
����Ŀ���Ķ�����գ�
Ѱ��ijЩ�������Ĺ��ɣ�
�Ŷ����κ�һ����֪�Ĺ�������������ͬ�����������͵õ���һ���µĹ����������磺![]() �����ǰ�������2����3�����ͷֱ�õ�
�����ǰ�������2����3�����ͷֱ�õ�![]() ��
��![]() ����������������11�����͵õ� ������������n�����͵õ� ��
����������������11�����͵õ� ������������n�����͵õ� ��
�ƶ�������һ������1�����������������й�������
��������Ϊ3��4��5����Ϊ������![]() ��
��
��������Ϊ5��12��13������![]() ��
��
��������Ϊ7��24��25������ ������
��������Ϊm(mΪ����)��n�� ������m2= ����m����ʾn�� ��
��m=17ʱ����n�� ����ʱ������Ϊ ��
�Ƕ��ڴ���4��ż����
��������Ϊ6��8��10����Ϊ![]() �����С������ҳ���Щ������֮��Ĺ�ϵ�������ʵ�����ĸ��ʾ�����Ĺ�����������ż��Ϊ24�Ĺ�������
�����С������ҳ���Щ������֮��Ĺ�ϵ�������ʵ�����ĸ��ʾ�����Ĺ�����������ż��Ϊ24�Ĺ�������
���𰸡���1��![]() ��
��![]() ;
;
��2��72+242=252��n+1��2n+1��![]() ��144����17��144��145����
��144����17��144��145����
��3��![]() ��
��![]() ����m=24ʱ��n=143��������Ϊ24��143��145.
����m=24ʱ��n=143��������Ϊ24��143��145.
��������
��1��������֪�����ҳ������������õĹ��ɼ����������2��������֪�����ҳ������������õĹ��ɼ����������3����![]() ��
��![]() ��
��![]() ��
��![]() ���ɵ�
���ɵ�![]() ��
��![]() �������m=24ʱ�Ĺ���������.
�������m=24ʱ�Ĺ���������.
��1����32+42=52����������2����3�����ͷֱ�õ�62+82=102��92+122=152����
���������11�����͵õ�332+442=552������������n����nΪ�����������͵õ���3n��2+��4n��2=��5n��2��
�ʴ�Ϊ��332+442=552����3n��2+��4n��2=��5n��2��
��2����������Ϊ3��4��5������![]() ��������Ϊ5��12��13������
��������Ϊ5��12��13������![]() ��
��
�����Ϊ7��24��25������72+242=252��������Ϊm(mΪ����)��n��n+1������m2=![]() ����m����ʾn��
����m����ʾn�� ![]() ��
��
����m=17ʱ����n��144����ʱ������Ϊ17��144��145��
�ʴ�Ϊ��72+242=252��n+1��2n+1��![]() ��144����17��144��145����
��144����17��144��145����
��3����![]() ��
��![]() ��
��![]() ��
��![]() ����
����
��![]() ��
��![]() ��
��
��m=24ʱ��n=143��������Ϊ24��143��145.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����,��ʦ����һ����:����
[8(a+b)5-4(a+b)4+(-a-b)3]��[2(a+b)3].
С��ͬѧ���Ͼ���,������С���Ľ������:
[8(a+b)5-4(a+b)4+(-a-b)3]��[2(a+b)3]
=[8(a+b)5-4(a+b)4+(a+b)3]��8(a+b)3
=(a+b)2-![]() (a+b)+
(a+b)+ ![]() .
.
С��Ҳ��������,˵С���Ľ�����̲���,��ָ�˳���.��ʦ�϶���С���Ļش�.��֪��С�������Ķ���?��ָ����,��д����ȷ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=8��BC=10����BΪԲ�ģ����ⳤΪ�뾶�����ֱ�BA��BC�ڵ�M��N���ٷֱ���M��NΪԲ�ģ����� ![]() MN��Ϊ�뾶�������������ڵ�P������BP���ӳ���AC�ڵ�D������BDC�����Ϊ20�����ABD�����Ϊ�� ��
MN��Ϊ�뾶�������������ڵ�P������BP���ӳ���AC�ڵ�D������BDC�����Ϊ20�����ABD�����Ϊ�� �� 
A.20
B.18
C.16
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��

��1��2018�ڵ�________������________����
��2�����������ɵ���![]() ������
������
�� ��������ĺͿ�����2019����Ϊʲô��
�� �����������ĺ���60��ֱ��д�����������
��3�������������ĺ��ܷ���2025�������������5��������������˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y= ![]() x+1��������y=ax2+bx��3����A��B���㣬��A��x���ϣ���B��������Ϊ3����P��ֱ��AB�·�����������һ���㣨����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB���C����PD��AB�ڵ�D
x+1��������y=ax2+bx��3����A��B���㣬��A��x���ϣ���B��������Ϊ3����P��ֱ��AB�·�����������һ���㣨����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB���C����PD��AB�ڵ�D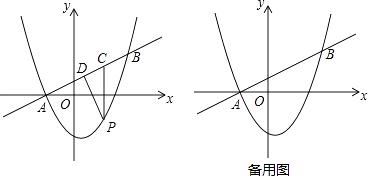
��1�����������ߵĽ���ʽ������sin��ACP��ֵ
��2�����P�ĺ�����Ϊm
���ú�m�Ĵ���ʽ��ʾ�߶�PD�ij���������߶�PD�������ֵ��
������PB���߶�PC�ѡ�PDB�ֳ����������Σ���������������������֮��Ϊ9��10ʱ��mֵ��
���Ƿ�����ʺϵ�mֵ��ʹ��PCD���PBD���ƣ������ڣ�ֱ��д��mֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ���A��ʾ��a����B��ʾ��b����ѧϰ����ֵʱ������֪���˾���ֵ�ļ��κ��壺
������A��B֮��ľ������|AB|�����壺|AB|��|a��b|���磺|a+6|��ʾ��a�ͩ�6�������϶�Ӧ������֮��ľ��룮|a��1|��ʾ��a��1�������϶�Ӧ������֮��ľ��룮
��1����a����|a+6|+|a+4|+|a��1|��ֵ��С��b��3a��Ϊ�෴����ֱ��д����A��Ӧ������ ������B��Ӧ������ ����
��2���ڣ�1���������£���֪��E�ӵ�A������1��λ/����ٶ������˶���ͬʱ��F�ӵ�B������2��λ/����ٶ������˶���FO���е�Ϊ��P�������н��ۣ���PO+AE��ֵ���䣻��PO��AE��ֵ���䣬��������ֻ��һ������ȷ�ģ�ѡ����������ֵ��
��3���ڣ�1���������£���֪����M��A�������1��λ/����ٶ������˶�������N��B�������3��λ/����ٶ������˶�������T��ԭ���λ�ó�����x��λ/����ٶ������˶�����������ͬʱ���������˶������������Ⱥ��������TM��TN������������μ����ʱ��Ϊ4�룬������������x��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬʱ�������ʵؾ��ȵ����ӣ��۲�����һ��ĵ������������ӵĵ�����ͬ�ĸ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶Ϊ����ѧϰ��ȤС�飬�����ġ���ѧ��Ӣ���������ѧ��˼��Ʒ�¡���ʷ���ۺϹ��˸���Ŀ��ϲ����������ʾ����飨ÿ��ֻѡһ����±��������ȡ����ѧ�����ʾ�����ͳ�ƵĽ����
��Ŀ | ���� | ��ѧ | Ӣ�� | ���� | ��ѧ | ˼��Ʒ�� | ��ʷ | �ۺ� |
���� | 6 | 10 | 11 | 12 | 10 | 9 | 8 | 14 |

���ݱ�����Ϣ������������⣺
��1�������������ѧ�������ˣ�
��2�������������ѧ���У�ϲ����Ŀ��������ࣻ
��3�������ϱ��е����ݲ�ȫ����ͳ��ͼ��
��4�������У���꼶��600��ѧ������ô���Ƹ�У���꼶ϲ���ۺϿ�Ŀ��ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ABC�ı�AC��x���ϣ���BC��x�ᣬ˫����y= ![]() ���BC���ڵ�D��4��m�������AB���ڵ�E��2��n����
���BC���ڵ�D��4��m�������AB���ڵ�E��2��n����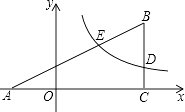
��1����n����m�ĺ�����ϵʽ��
��2����BD=2��tan��BAC= ![]() ����k��ֵ�͵�B�����꣮
����k��ֵ�͵�B�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com