
����Ŀ���������ϣ���A��ʾ��a����B��ʾ��b����ѧϰ����ֵʱ������֪���˾���ֵ�ļ��κ��壺
������A��B֮��ľ������|AB|�����壺|AB|��|a��b|���磺|a+6|��ʾ��a�ͩ�6�������϶�Ӧ������֮��ľ��룮|a��1|��ʾ��a��1�������϶�Ӧ������֮��ľ��룮
��1����a����|a+6|+|a+4|+|a��1|��ֵ��С��b��3a��Ϊ�෴����ֱ��д����A��Ӧ������ ������B��Ӧ������ ����
��2���ڣ�1���������£���֪��E�ӵ�A������1��λ/����ٶ������˶���ͬʱ��F�ӵ�B������2��λ/����ٶ������˶���FO���е�Ϊ��P�������н��ۣ���PO+AE��ֵ���䣻��PO��AE��ֵ���䣬��������ֻ��һ������ȷ�ģ�ѡ����������ֵ��
��3���ڣ�1���������£���֪����M��A�������1��λ/����ٶ������˶�������N��B�������3��λ/����ٶ������˶�������T��ԭ���λ�ó�����x��λ/����ٶ������˶�����������ͬʱ���������˶������������Ⱥ��������TM��TN������������μ����ʱ��Ϊ4�룬������������x��ֵ��

���𰸡���1����A��Ӧ������4����B��Ӧ����12����2��PO��AE��ֵ���䣻��3������������x��ֵΪ2
��������
��1��a����|a+6|+|a+4|+|a��1|��ֵ��С��������a�ͩ�6��a�ͩ�4��a��1�������϶�Ӧ������֮��ľ���֮����С������a����4��b��12����2�����˶�ʱ��Ϊt�룬������������PO��AE�ij������м��㼴�ɣ���3�����˶�ʱ��Ϊt�룬��������TM��TN���Ҽ����ʱ��Ϊ4�룬�г������鼴��.
��1��a����|a+6|+|a+4|+|a��1|��ֵ��С��������a�ͩ�6��a�ͩ�4��a��1�������϶�Ӧ������֮��ľ���֮����С��
��a����4��b��12
���A��Ӧ������4����B��Ӧ����12
��2��PO��AE��ֵ����
���˶�ʱ��Ϊt�룬��������ɵã�BF��2t��AE��t����OF��12+2t
��FO���е�Ϊ��P
��OP��6+t
��PO��AE��6+t��t��6
PO��AE��ֵ����
��3�����˶�ʱ��Ϊt�룬��AM��t��OT��xt��BN��3t
���ݵ�һ��TM��TN�ã�xt+12��3t��4+t��xt
���ݵڶ���TM��TN�ã�x��t+4����{3��t+4����12}��4+��4+t����x��4+t��
��ʽ�����ã�x��2
������������x��ֵΪ2


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬ƽ���ı���ABOC�ĶԽ��߽��ڵ�M��˫����y= ![]() ��x��0��������B��M����ƽ���ı���ABOC�����Ϊ12����k= ��
��x��0��������B��M����ƽ���ı���ABOC�����Ϊ12����k= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ4������ABCD�У���A=60�㣬M��AD�ߵ��е㣬��N��AB����һ���㣬����AMN��MN���ڵ�ֱ�߷��۵õ���A��MN������A��C�����߶�A��C���ȵ���Сֵ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ2�����������У���������Բ����������Բ�������������������Բ�����е�Բ�����ڲ���ȥ�����������ʣ�²��֣���Ӱ���֣������Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����գ�
Ѱ��ijЩ�������Ĺ��ɣ�
�Ŷ����κ�һ����֪�Ĺ�������������ͬ�����������͵õ���һ���µĹ����������磺![]() �����ǰ�������2����3�����ͷֱ�õ�
�����ǰ�������2����3�����ͷֱ�õ�![]() ��
��![]() ����������������11�����͵õ� ������������n�����͵õ� ��
����������������11�����͵õ� ������������n�����͵õ� ��
�ƶ�������һ������1�����������������й�������
��������Ϊ3��4��5����Ϊ������![]() ��
��
��������Ϊ5��12��13������![]() ��
��
��������Ϊ7��24��25������ ������
��������Ϊm(mΪ����)��n�� ������m2= ����m����ʾn�� ��
��m=17ʱ����n�� ����ʱ������Ϊ ��
�Ƕ��ڴ���4��ż����
��������Ϊ6��8��10����Ϊ![]() �����С������ҳ���Щ������֮��Ĺ�ϵ�������ʵ�����ĸ��ʾ�����Ĺ�����������ż��Ϊ24�Ĺ�������
�����С������ҳ���Щ������֮��Ĺ�ϵ�������ʵ�����ĸ��ʾ�����Ĺ�����������ż��Ϊ24�Ĺ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������
��1������6����|��![]() |������1��3������7��
|������1��3������7��
��2����23��[����![]() ��+
��+![]() ]��6������
]��6������![]() ��2��
��2��![]() ����
����![]() ��+����
��+����![]() ��
��
��3��![]() x��2��x��
x��2��x��![]() ��+����
��+����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���BAC=90�㣬AB=3��AC=4��ADƽ�֡�BAC��BC��D����BD�ij�Ϊ�������� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��AB���O������B�㣬C�ǡ�O��OA�Ľ��㣬��D�ǡ�O�ϵĶ��㣨D��B��C���غϣ�������A=40�㣬���BDC�Ķ����ǣ�������
A.25���155��
B.50���155��
C.25���130��
D.50���130��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c��y���ڵ�C��0��4�����Գ���x=2��x�ύ�ڵ�D������ΪM����DM=OC+OD��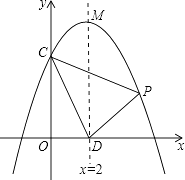
��1����������ߵĽ���ʽ��
��2�����P��x��y���ǵ�һ�����ڸ��������ϵ�һ�����㣬��PCD�����ΪS����S����x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3���ڣ�2���������£���������P��ֱ��PE��y�ύ�ڵ�E���Ƿ������O��P��EΪ��������������OPDȫ�ȣ������ڣ������ֱ��PE�Ľ���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com