
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD.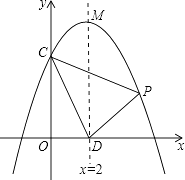
(1)求该抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,若经过点P的直线PE与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出直线PE的解析式;若不存在,请说明理由.
【答案】
(1)
解:由题意得:OC=4,OD=2,
∴DM=OC+OD=6,
∴顶点M坐标为(2,6).
设抛物线解析式为:y=a(x﹣2)2+6,
∵点C(0,4)在抛物线上,
∴4=4a+6,
解得a= ![]() .
.
∴抛物线的解析式为:y= ![]() (x﹣2)2+6=
(x﹣2)2+6= ![]() x2+2x+4.
x2+2x+4.
(2)
解:如答图1,过点P作PE⊥x轴于点E.
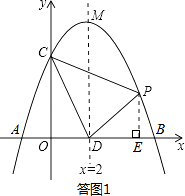
∵P(x,y),且点P在第一象限,
∴PE=y,OE=x,
∴DE=OE﹣OD=x﹣2.
S=S梯形PEOC﹣S△COD﹣S△PDE
= ![]() (4+y)x﹣
(4+y)x﹣ ![]() ×2×4﹣
×2×4﹣ ![]() (x﹣2)y
(x﹣2)y
=y+2x﹣4.
将y= ![]() x2+2x+4代入上式得:S=
x2+2x+4代入上式得:S= ![]() x2+2x+4+2x﹣4=
x2+2x+4+2x﹣4= ![]() x2+4x.
x2+4x.
在抛物线解析式y= ![]() x2+2x+4中,令y=0,即
x2+2x+4中,令y=0,即 ![]() x2+2x+4=0,解得x=2±
x2+2x+4=0,解得x=2± ![]() .
.
设抛物线与x轴交于点A、B,则B(2+ ![]() ,0),
,0),
∴0<x<2+ ![]() .
.
∴S关于x的函数关系式为:S= ![]() x2+4x(0<x<2+
x2+4x(0<x<2+ ![]() ).
).
(3)
解:存在.
若以O、P、E为顶点的三角形与△OPD全等,可能有以下情形:
(Ⅰ)OD=OP.
由图象可知,OP最小值为4,即OP≠OD,故此种情形不存在.
(Ⅱ)OD=OE.
若点E在y轴正半轴上,如答图2所示:

此时△OPD≌△OPE,
∴∠OPD=∠OPE,即点P在第一象限的角平分线上,
所以P点的横纵坐标相等,即 ![]() x2+2x+4=x,解答x1=﹣2(舍去),x2=4.
x2+2x+4=x,解答x1=﹣2(舍去),x2=4.
所以P点坐标为:(4,4),
∴直线PE的解析式为:y= ![]() x+2;
x+2;
若点E在y轴负半轴上,易知此种情形下,两个三角形不可能全等,故不存在.
(Ⅲ)OD=PE.
∵OD=2,
∴第一象限内对称轴右侧的点到y轴的距离均大于2,
则点P只能位于对称轴左侧或与顶点M重合.
若点P位于第一象限内抛物线对称轴的左侧,易知△OPE为钝角三角形,而△OPD为锐角三角形,则不可能全等;
若点P与点M重合,如答图3所示,此时△OPD≌OPE,四边形PDOE为矩形,

∴直线PE的解析式为:y=6.
综上所述,存在以O、P、E为顶点的三角形与△OPD全等,直线PE的解析式为y=6,y= ![]() x+2.
x+2.
【解析】(1)首先求出点M的坐标,然后利用顶点式和待定系数法求出抛物线的解析式;(2)如答图1所示,作辅助线构造梯形,利用S=S梯形PEOC﹣S△COD﹣S△PDE求出S关于x的表达式;求出抛物线与x轴正半轴的交点坐标,得到自变量的取值范围;(3)由于三角形的各边,只有OD=2是确定长度的,因此可以以OD为基准进行分类讨论:①OD=OP.因为第一象限内点P到原点的距离均大于4,因此OP≠OD,此种情形排除;②OD=OE.分析可知,只有如答图2所示的情形成立;③OD=PE.分析可知,只有如答图3所示的情形成立.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】在数轴上,点A表示数a,点B表示数b,在学习绝对值时,我们知道了绝对值的几何含义:
数轴上A、B之间的距离记作|AB|,定义:|AB|=|a﹣b|.如:|a+6|表示数a和﹣6在数轴上对应的两点之间的距离.|a﹣1|表示数a和1在数轴上对应的两点之间的距离.
(1)若a满足|a+6|+|a+4|+|a﹣1|的值最小,b与3a互为相反数,直接写出点A对应的数 ,点B对应的数 .
(2)在(1)的条件下,已知点E从点A出发以1单位/秒的速度向右运动,同时点F从点B出发以2单位/秒的速度向右运动,FO的中点为点P,则下列结论:①PO+AE的值不变;②PO﹣AE的值不变,其中有且只有一个是正确的,选出来并求其值.
(3)在(1)的条件下,已知动点M从A点出发以1单位/秒的速度向左运动,动点N从B点出发以3单位/秒的速度向左运动,动点T从原点的位置出发以x单位/秒的速度向左运动,三个动点同时出发,若运动过程中正好先后出现两次TM=TN的情况,且两次间隔的时间为4秒,求满足条件的x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(a,1)、B(﹣1,b)都在双曲线y=﹣ ![]() 上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )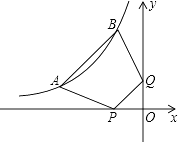
A.y=x
B.y=x+1
C.y=x+2
D.y=x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的边AC在x轴上,边BC⊥x轴,双曲线y= ![]() 与边BC交于点D(4,m),与边AB交于点E(2,n).
与边BC交于点D(4,m),与边AB交于点E(2,n).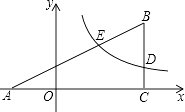
(1)求n关于m的函数关系式;
(2)若BD=2,tan∠BAC= ![]() ,求k的值和点B的坐标.
,求k的值和点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市自从去年九月实施高中新课程改革以来,高中学生在课堂上的“自主学习、合作交流”能力有了很大提高.张老师为了了解所教班级学生的“自主学习、合作交流”的具体情况,对该班部分学生进行了为期一个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差,且将调查结果绘制成以下两幅不完整的统计图.请你根据统计图解答下列问题: 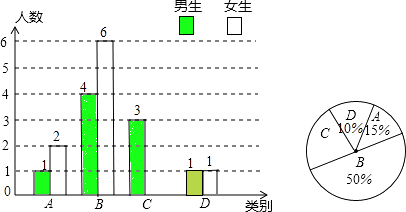
(1)本次调查中,张老师一共调查了多少名学生,其中C类女生有多少名;
(2)请将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.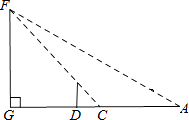
(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上, ![]() ,结果精确到0.1)
,结果精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com