
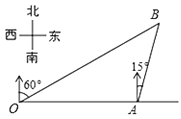
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测点O处测得该船位于北偏东60°的方向,则该船航行的距离为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】小明解不等式![]() 的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
解:去分母,得3(1+x)-2(2x+1)≤1.①
去括号,得3+3x-4x+1≤1.②
移项,得3x-4x≤1-3-1.③
合并同类项,得-x≤-3.④
两边都除以-1,得x≤3.⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由.
解: ,理由如下:
∵AB∥CD,
∴∠B=∠BCD,( )
∵∠B=70°,
∴∠BCD=70°,( )
∵∠BCE=20°,
∴∠ECD=50°,
∵∠CEF=130°,
∴ + =180°,
∴EF∥ ,( )
∴AB∥EF.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等边三角形.
(1)如图,点D在AB边上,点E在AC边上,BD=CE,BE与CD交于点F.试判断BF与CF的数量关系,并加以证明;
(2)点D是AB边上的一个动点,点E是AC边上的一个动点,且BD=CE,BE与CD交于点F.若△BFD是等腰三角形,求∠FBD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定对居民生活用电实行“阶梯电价”收费,具体收费标准见表:
一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
不超过200度 | a |
超过200度的部分 | b |
已知4月份,该市居民甲用电250度,交电费130元;居民乙用电400度,交电费220元.
(1)求出表中a和b的值;
(2)实行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价每度不超过0.56元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥市某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区100个家庭收入按从高到低是5800,……,10000元各不相同,在输入计算时,把最大的数错误地输成100000元,则依据错误的数据算出的平均数比实际平均数多( )
A. 900元B. 942元C. 90000元D. 9000元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为( ).
A.3
B.![]()
C.5
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com