
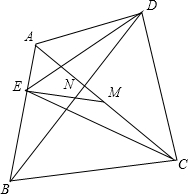
 如图,凸四边形ABCD中,M、N分别是对角线AC、BD的中点,MN交AB于E.求证:S△CDE=$\frac{1}{2}$SABCD.
如图,凸四边形ABCD中,M、N分别是对角线AC、BD的中点,MN交AB于E.求证:S△CDE=$\frac{1}{2}$SABCD. 分析 连接DM,BM,由M、N分别是对角线AC、BD的中点,又根据等底同高的三角形的面积相等,得到S△CDM=S△ADM,S△DEN=S△BEN,S△ECM=S△AEM,S△MDN=S△BMN,然后根据等式的性质得到即可得到结论.
解答 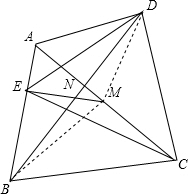 解:连接DM,BM,
解:连接DM,BM,
∵M、N分别是对角线AC、BD的中点,
∴S△CDM=S△ADM,S△DEN=S△BEN,S△ECM=S△AEM,S△MDN=S△BMN,
∴S△CDM+S△DEN+S△ECM+S△MDN=S△ADM+S△BEN+S△AEM+S△BMN,
∴S△DEC=S△ADM+S△ABM=$\frac{1}{2}$S△ACD+$\frac{1}{2}$S△ABC=$\frac{1}{2}$S四边形ABCD.
点评 本题考查了等底同高的三角形的面积相等,等式的性质,知道等底等高的两三角形面积相等是解题的关键.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
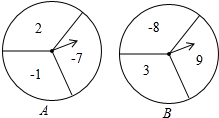 如图,两个可以自由转动的均匀转盘,A、B都被平均分成了3份,并在每份内标有一个有理数.有如下游戏规则:
如图,两个可以自由转动的均匀转盘,A、B都被平均分成了3份,并在每份内标有一个有理数.有如下游戏规则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,某海军基地位于A处,在其正南方向100海里处有一重要目标B,在B的正东方向100海里处也有一重要目标C,小岛D位于AC的中点,岛上有一补给码头,一艘军舰从A出发,经B到C匀速航行,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰,已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇,那么相遇时补给船航行了多少海里(结果精确到0.1海里)?
如图所示,某海军基地位于A处,在其正南方向100海里处有一重要目标B,在B的正东方向100海里处也有一重要目标C,小岛D位于AC的中点,岛上有一补给码头,一艘军舰从A出发,经B到C匀速航行,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰,已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇,那么相遇时补给船航行了多少海里(结果精确到0.1海里)?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
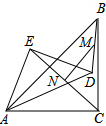 已知等腰Rt△ABC和等腰Rt△ABC中,∠ACB=∠AED=90°,且AD=AC,若点M、N分别是DB、EC的中点,证明:MN⊥EC,MN=$\frac{1}{2}$EC.
已知等腰Rt△ABC和等腰Rt△ABC中,∠ACB=∠AED=90°,且AD=AC,若点M、N分别是DB、EC的中点,证明:MN⊥EC,MN=$\frac{1}{2}$EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com