练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】同一平面内的两条线段，下列说法正确的是(　　)

    A. 一定平行

    B. 一定相交

    C. 可以既不平行又不相交

    D. 不平行就相交

    【答案】C

    【解析】

    根据线段有固定长度这一特点来解题即可.

    同一平面内的两条线段，可以出现相交，平行，也可以出现既不平行也不相交的状态.

    故选C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=kx+b与双曲线（x﹤0）相交于A（-4，a）、B（-1，4）两点.

    （1）求直线和双曲线的解析式；

    （2）在y轴上存在一点P，使得PA+PB的值最小，求点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列有关圆的一些结论：①与半径长相等的弦所对的圆周角是30°；②圆内接正六边形的边长与该圆半径相等；③垂直于弦的直径平分这条弦；④平分弦的直径垂直于弦．其中正确的是（ ）
    A.①②③
    B.①③④
    C.②③
    D.②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程.

    （1）若该方程的一个根为2，求a的值及该方程的另一根.

    （2）求证：不论a取何实数，该方程都有两个不相等的实数根.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列叙述中，正确的是（　　）

    A. 在同一平面内，两条直线的位置关系有三种，分别是相交、平行、垂直

    B. 不相交的两条直线叫平行线

    C. 两条直线的铁轨是平行的

    D. 我们知道，对顶角是相等的，那么反过来，相等的角就是对顶角

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法中，错误的是（　　）

    A.菱形的对角线互相垂直平分

    B.正方形的对角线互相垂直平分且相等

    C.矩形的对角线相等且平分

    D.平行四边形的对角线相等且垂直

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ 中，点 ， ， 分别是边 ， ， 的中点，且 .

    （1）求证：四边形 为矩形；
    （2）若 ， ，写出矩形 的周长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于正数 ，用符号 表示 的整数部分，例如： ， ， ．点 在第一象限内，以A为对角线的交点画一个矩形，使它的边分别与两坐标轴垂直. 其中垂直于 轴的边长为 ，垂直于 轴的边长为 ，那么，把这个矩形覆盖的区域叫做点A的矩形域．例如：点 的矩形域是一个以 为对角线交点，长为3，宽为2的矩形所覆盖的区域，如图1所示，它的面积是6．

    图1 图2
    根据上面的定义，回答下列问题：
    （1）在图2所示的坐标系中画出点 的矩形域，该矩形域的面积是；
    （2）点 的矩形域重叠部分面积为1，求 的值；
    （3）已知点 在直线 上， 且点B的矩形域的面积 满足 ，那么 的取值范围是 ． （直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平面直角坐标系xOy中，B ， C两点的坐标分别为 ， ，CD⊥y轴于点D ， 直线l 经过点D.

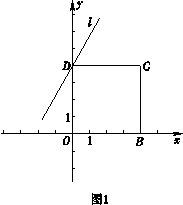
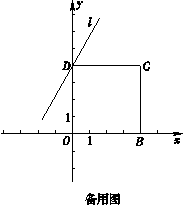
    （1）直接写出点D的坐标；
    （2）作CE⊥直线l于点E ， 将直线CE绕点C逆时针旋转45°，交直线l于点F ， 连接BF.
    ①依题意补全图形；
    ②通过观察、测量，同学们得到了关于直线BF与直线l的位置关系的猜想，请写出你的猜想；
    ③通过思考、讨论，同学们形成了证明该猜想的几种思路：
    思路1：作CM⊥CF ， 交直线l于点M ， 可证△CBF≌△CDM ， 进而可以得出 ，从而证明结论.
    思路2：作BN⊥CE ， 交直线CE于点N ， 可证△BCN≌△CDE ， 进而证明四边形BFEN为矩形，从而证明结论.
    ……
    请你参考上面的思路完成证明过程.（一种方法即可）

    查看答案和解析>>

    同步练习册答案