
【题目】如图,直线y=kx+b与双曲线![]() (x﹤0)相交于A(-4,a)、B(-1,4)两点.
(x﹤0)相交于A(-4,a)、B(-1,4)两点.

(1)求直线和双曲线的解析式;
(2)在y轴上存在一点P,使得PA+PB的值最小,求点P的坐标.
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】(10分)某体育用品专卖店销售7个篮球和9个排球的总利润为355元,销售10个篮球和20个排球的总利润为650元.
(1)求每个篮球和每个排球的销售利润;
(2)已知每个篮球的进价为200元,每个排球的进价为160元,若该专卖店计划用不超过17400元购进篮球和排球共100个,且要求篮球数量不少于排球数量的一半,请你为专卖店设计符合要求的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下利事件中,是随机事件的是( )
A.通常温度降到0℃以下,纯净的水结冰
B.明天太阳从东边升起
C.购买一张彩票,中奖
D.任意画一个三角形,其内角和为360°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:

(1)本次被调查的学生有 名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6,AC=10,点D , E , F分别是AB , BC , AC的中点,则四边形ADEF的周长为( ).
A.16
B.12
C.10
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,四边形ABCD是平行四边形
求作:菱形AECF,使E,F分别在BC,AAD上
小凯的作法如下:
⑴连接AC
⑵作AC的垂直平分线EF分别交BC,AD于E,F
⑶连接AE,CF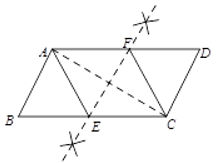
所以四边形AECF是菱形
老师说:“小凯的作法正确.”
请回答:在小凯的作法中,判定四边形AECF是菱形的依据是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com