
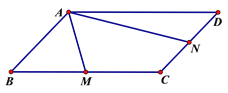
【题目】如图,在平行四边形ABCD中,M、N分别为BC、CD的中点,AM=1,AN=2,∠MAN=60°则AB的长为____________.
【答案】![]()
【解析】首先延长DC和AM交于E,过点E作EH⊥AN于点H,易证△ABM≌△ECM,则AM=EM=1,AN=2,且∠MAN=60°,求得AH,NH与EH的长,从而求得NE的长,则可求得答案.
解:(解法一)延长DC和AM交于E,过点E作EH⊥AN于点H,
∵ABCD为平行四边形
∴AB∥CE,
∴∠BAM=∠MEC,∠ABM=∠ECM,
∵M为BC的中点,
∴BM=MC,
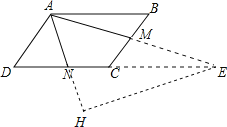
∴△ABM≌△ECM,
∴AB=CD=CE,AM=EM=2,
∵N为DC的中点,
∴NE=3NC=![]() AB,即AB=
AB,即AB=![]() NE,
NE,
∵AN=2,AE=2AM=4,且∠MAN=60°,
∴∠AEH=30°,
∴AH=![]() AE=2,
AE=2,
∴EH=![]() ,
,
∴NH=AH-AN=2-1=1,
∴EN=![]() ,
,
∴AB=![]() .
.
解法二:延长DC和AM交于E,根据平行四边形的性质可得出∠BAM=∠MEC,∠ABM=∠ECM,可证明△ABM≌△ECM,则AM=EM=2,由N为边DC的中点,得NR=3NC=1.5AB,AB=![]() NE,由余弦定理可解得EN,从而得出AB即可.
NE,由余弦定理可解得EN,从而得出AB即可.
解:延长DC和AM交于E,
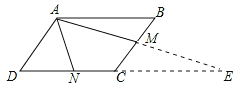
∵ABCD为平行四边形
∴AB∥CE,
∴∠BAM=∠MEC,∠ABM=∠ECM,
∵M为BC的中点,
∴BM=MC,
∴△ABM≌△ECM,
∴AB=CD=CE,AM=EM=2,
∵N为DC的中点,
∴NE=3NC=1.5AB即AB=![]() NE,
NE,
∵AN=2,AE=2AM=4,且∠MAN=60°,
由余弦定理EN2=AE2+AN2-2AE×ANcos60°=16+1-2×4×![]() =13,
=13,
∴EN=![]() ,
,
∴AB=![]() .
.
故答案为: ![]() .
.
“点睛”本题考查了平行线的性质、勾股定理以及三角形的中位线定理,是中考常见的题型,难度偏大.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形 ![]() 中,点
中,点 ![]() 是
是 ![]() 边上任意一点,连接
边上任意一点,连接 ![]() .过点
.过点 ![]() 作线段
作线段 ![]() 的平行线,交
的平行线,交 ![]() 延长线于点
延长线于点 ![]() .
.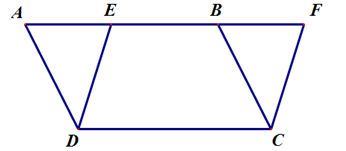
(1)证明: ![]() .
.
(2)过点 ![]() 作
作 ![]() ,垂足为点
,垂足为点 ![]() .点
.点 ![]() 为
为 ![]() 边中点,连接
边中点,连接 ![]() ,
, ![]() .
.
① 根据题意完成作图;
② 猜想线段 ![]() ,
, ![]() 的数量关系,并写出你的证明思路.
的数量关系,并写出你的证明思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 两条不相交的直线叫做平行线
B. 一条直线的平行线有且只有一条
C. 若直线a∥b,a∥c,则b∥c
D. 若两条线段不相交,则它们互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)若DH=![]() ,求EF的长和半径OA的长.
,求EF的长和半径OA的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b与双曲线![]() (x﹤0)相交于A(-4,a)、B(-1,4)两点.
(x﹤0)相交于A(-4,a)、B(-1,4)两点.

(1)求直线和双曲线的解析式;
(2)在y轴上存在一点P,使得PA+PB的值最小,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com