
【题目】如图,在平行四边形 ![]() 中,点
中,点 ![]() 是
是 ![]() 边上任意一点,连接
边上任意一点,连接 ![]() .过点
.过点 ![]() 作线段
作线段 ![]() 的平行线,交
的平行线,交 ![]() 延长线于点
延长线于点 ![]() .
.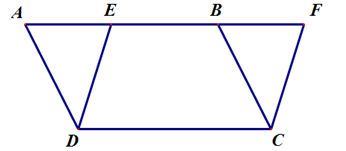
(1)证明: ![]() .
.
(2)过点 ![]() 作
作 ![]() ,垂足为点
,垂足为点 ![]() .点
.点 ![]() 为
为 ![]() 边中点,连接
边中点,连接 ![]() ,
, ![]() .
.
① 根据题意完成作图;
② 猜想线段 ![]() ,
, ![]() 的数量关系,并写出你的证明思路.
的数量关系,并写出你的证明思路.
【答案】
(1)
证明:∵四边形 ![]() 是平行四边形
是平行四边形
∴ ![]() ,
, ![]()
又∵ ![]()
∴四边形 ![]() 是平行四边形
是平行四边形
∴ ![]()
∴ ![]()
∴ ![]()
∴ ![]()
(2)
解:①作图:
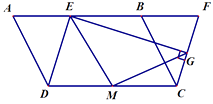
②猜想: ![]() ;
;
证明思路:
延长 ![]() ,
, ![]() 交于点
交于点 ![]()
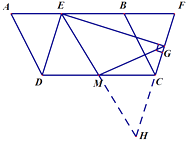
证明 ![]()
得到 ![]()
在 ![]() 中,得到
中,得到 ![]()
【解析】(1)由平行四边形的性质得AB=CD , AB∥CD;由两组对边分别平行得四边形 DEFC 是平行四边形;由平行四边形的性质得EF=CD;
由等量代换得 AE=BF;
(2)①如图;②猜想: M E = M G ;延长 EM , FC 交于点 H由已知条件证明△DEM≌△CHM,由全等三角形的性质得ME=MH;在 Rt△EHG 中,得到 ME=MG.
【考点精析】利用直角三角形斜边上的中线和平行四边形的判定与性质对题目进行判断即可得到答案,需要熟知直角三角形斜边上的中线等于斜边的一半;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于CE于点F,交CD于点G(如图l),求证:AE=CG; 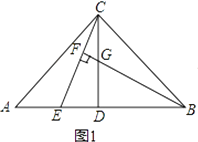
(2)直线AH垂直于CE,垂足为H,交CD的延长线于点M(如图2),找出图中与BE相等的线段(不需要添加辅助线),并说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区环保部门为了提高宣传垃圾分类的实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,进行整理后,绘制了如下两幅不完整的统计图: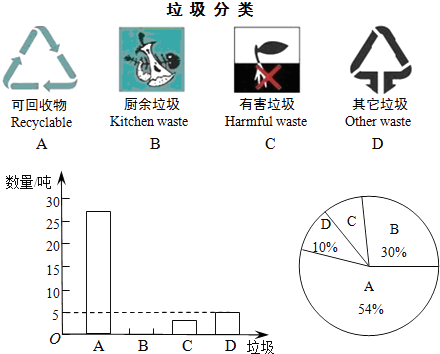
根据统计图解答下列问题:
(1)求抽样调查的生活垃圾的总吨数以及其中的有害垃圾的吨数;
(2)求扇形统计图中,“D”部分所对应的圆心角的度数,并将条形统计图补充完整;
(3)调查发现,在可回收物中废纸垃圾约占 ![]() ,每回收1吨废纸可再造0.85吨的再生纸,假设该城市每月生产的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可制成再生纸多少吨?
,每回收1吨废纸可再造0.85吨的再生纸,假设该城市每月生产的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可制成再生纸多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
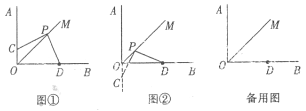
【题目】已知∠AOB=90°,OM是∠AOB的平分线,点D是边OB上一定点,将三角板的直角顶点P在射线OM上移动,使一直角边经过点D,另一直角与边OA交于点C.容易证得PC=PD(如图①)
(1)若另一直角边与边OA的反向延长线相交于点C(如图②),试问PC与PD还会相等吗?若相等,请予以证明;若不相等,请说明理由;
(2)已知OD=4,三角板在移动过程中,另一直角边与直线OA,直线OB分别交于点C,E,且以P,D,E为顶点的三角形与OCD相似,试求线段OP的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某体育用品专卖店销售7个篮球和9个排球的总利润为355元,销售10个篮球和20个排球的总利润为650元.
(1)求每个篮球和每个排球的销售利润;
(2)已知每个篮球的进价为200元,每个排球的进价为160元,若该专卖店计划用不超过17400元购进篮球和排球共100个,且要求篮球数量不少于排球数量的一半,请你为专卖店设计符合要求的进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com