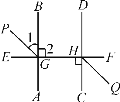
[题目]如图.AB⊥EF于点G.CD⊥EF于点H.GP平分∠EGB.HQ平分∠CHF.图中有哪些平行线?并说明理由．题目和参考答案——青夏教育精英家教网—

【题目】如图，AB⊥EF于点G，CD⊥EF于点H，GP平分∠EGB，HQ平分∠CHF，图中有哪些平行线？并说明理由．

【答案】AB∥CD，GP∥HQ.理由见解析

【解析】

根据垂直的性质,在同一平面内,垂直于同一条直线的两条直线平行, 因为AB⊥EF,CD⊥EF,所以AB∥CD ,再根据角平分线的定义可得: ∠1＝∠EGB＝45°,所以∠PGH＝∠1＋∠2＝135°,同理可得∠GHQ＝135°,根据内错角相等,两直线平行可得: GP∥HQ.

AB∥CD,GP∥HQ.理由如下:因为AB⊥EF,CD⊥EF,

所以AB∥CD(在同一平面内,垂直于同一条直线的两条直线平行),

因为AB⊥EF(已知),

所以∠EGB＝∠2＝90°(垂直定义)．

因为GP平分∠EGB(已知),

所以∠1＝∠EGB＝45°(角平分线的定义),

所以∠PGH＝∠1＋∠2＝135°,

同理可得∠GHQ＝135°,

所以∠PGH＝∠GHQ,所以GP∥HQ(内错角相等,两直线平行).

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】已知：△ABC，∠A、∠B、∠C之和为多少？为什么？

解：∠A+∠B+∠C=180°

理由：作∠ACD=∠A，并延长BC到E

∵∠ACD=∠　　（已作）

AB∥CD（　　）

∴∠B=　　（　　）

而∠ACB+∠ACD+∠DCE=180°

∴∠ACB+　　+　　=180°（　　）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知，抛物线y=ax2+bx+c（a≠0）经过原点，顶点为A（h，k）（h≠0）．
（1）当h=1，k=2时，求抛物线的解析式；
（2）若抛物线y=tx2（t≠0）也经过A点，求a与t之间的关系式；
（3）当点A在抛物线y=x2﹣x上，且﹣2≤h＜1时，求a的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，△ABC是等腰直角三角形，AC=BC=a，以斜边AB上的点O为圆心的圆分别与AC，BC相切于点E，F，与AB分别交于点G，H，且EH的延长线和CB的延长线交于点D，则CD的长为．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,

所以∠1=∠2.

所以______________∥　　　　(　　　　　　　　　).

因为AB与DE相交,

所以∠1=∠4(　　　　　).

所以∠4=65°.

又因为∠3=115°,

所以∠3+∠4=180°.

所以　　　　∥　　　　(　　　　　　　　　).

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】“保护好环境，拒绝冒黑烟”．某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车，计划购买A型和B型两种环保节能公交车共10辆，若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．
（1）求购买A型和B型公交车每辆各需多少万元？
（2）预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？哪种购车方案总费用最少？最少总费用是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，在ABCD中，∠ABC=60°，且AB=BC，∠MAN=60°．请探索BM，DN与AB的数量关系，并证明你的结论．