


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
 如图,在直角坐标系中,△ABC的顶点坐标是A(-1,2),B(-3,1),C(0,-1).将△ABC向右平移2个单位,向下平移3个单位得到△A1B1C1,将△A1B1C1绕O点旋转90°得到△A2B2C2.
如图,在直角坐标系中,△ABC的顶点坐标是A(-1,2),B(-3,1),C(0,-1).将△ABC向右平移2个单位,向下平移3个单位得到△A1B1C1,将△A1B1C1绕O点旋转90°得到△A2B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:
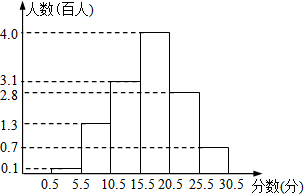 2014年3月28日是第19人全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如图“频数分布直方图”.请回答:
2014年3月28日是第19人全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如图“频数分布直方图”.请回答:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com