
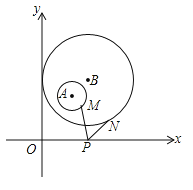
【题目】如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为
科目:初中数学 来源: 题型:
【题目】下列各组数中,不能作为直角三角形的三边长的是( )
A. 0.3,0.4,0.5 B. 8,9,10 C. 7,24,25 D. 9,12,15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动,小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查,她在300户家庭中,随机调查了50户家庭5月份的用水量情况,结果如图所示.

(1)试估计该小区5月份用水量不高于12 t的户数占小区总户数的百分比;
(2)把图中每组用水量的值用该组的中间值(如0~6的中间值为3)来替代,估计该小区5月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 关于中心对称的两个图形不一定全等
B. 全等的两个三角形必关于一个点对称
C. 一个中心对称图形只有一个对称中心
D. 平行四边形不是中心对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件属于不可能事件的是( )
A. 两个有理数的和是无理数
B. 从装有5个红球和1个白球的袋子中随机摸出1球是白球
C. 买一张电影票,座位号是偶数
D. 购买1张彩票中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为____ _____.
),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为____ _____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(备注:在直角三角形中30度角所对的边是斜边的一半)
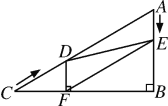
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果.甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计).问:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com