
����Ŀ����Rt��ABC�У���B=90����AC=60cm����A=60������D�ӵ�C������CA������4cm/����ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2cm/����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루0��t��15��������D��DF��BC�ڵ�F������DE��EF������ע����ֱ����������30�Ƚ����Եı���б�ߵ�һ�룩
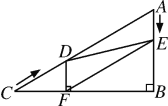
��1����֤��AE=DF��
��2���ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ�˵�����ɣ�
��3����tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
���𰸡���1����֤�����̼���������2����t=10����3����t=![]() ��12�����ɼ�����
��12�����ɼ�����
��������
�����������1��������Rt��ABC�����ʵó�AB=30cm������CD=4t��AE=2t�Լ�Rt��CDF�����ʵó��𰸣���2��������DF��AB��DF=AE���ó��ı���AEFD��ƽ���ı��Σ��������ε����ʵó�t��ֵ����3����������Ҫ����������ֱ���м���.����EDF=90��ʱ��AD=2AE���Ӷ����t��ֵ������DEF=90��ʱ��AE=2AD���Ӷ����t��ֵ.
�����������1��������Rt��ABC�У���C=90�㩁��A=30���� ��AB=![]() AC=
AC=![]() ��60=30cm
��60=30cm
��CD=4t��AE=2t�� ������Rt��CDF����C=30������DF=![]() CD=2t ��DF=AE
CD=2t ��DF=AE
��2�����ܡ�
��DF��AB��DF=AE�����ı���AEFD��ƽ���ı���
��AD=AEʱ���ı���AEFD�����Σ���60��4t=2t����ã�t=10
����t=10ʱ��AEFD������
��3��������DEFΪֱ�������Σ������������
����ͼ1����EDF=90����DE��BC��
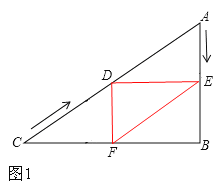
��AD=2AE����60��4t=2��2t����ã�t=![]() ��
��
����ͼ2����DEF=90����DE��AC��
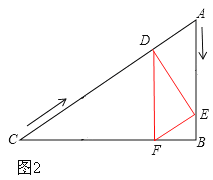
��AE=2AD����2t=2��60-4t������ã�t=12��
������������t=![]() ��12ʱ����DEFΪֱ��������
��12ʱ����DEFΪֱ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�����D��DE��AB���E����F�ڱ�CD�ϣ�DF=BE,����AF,BF

��1����֤���ı���BFDE�Ǿ��Σ�
��2����CF=3��BF=4��DF=5����֤��AFƽ����DAB.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У��ֱ��Ե�A��2��3������B��3��4��ΪԲ�ģ�1��3Ϊ�뾶����A����B��M��N�ֱ�����A����B�ϵĶ��㣬PΪx���ϵĶ��㣬��PM+PN����СֵΪ
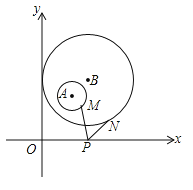
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�ĶԽ���AC��BD���ڵ�O ,AEƽ����BAD��BC�ڵ�E ,����ADC=600��AB=![]() BC ,����OE .���� ���ۣ��١�CAD=300 �� S��ABCD=ABAC �� OB=AB �� OE=
BC ,����OE .���� ���ۣ��١�CAD=300 �� S��ABCD=ABAC �� OB=AB �� OE=![]() BC �����ĸ����У� ��
BC �����ĸ����У� ��
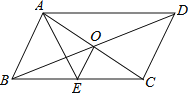
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
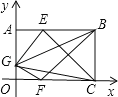
����Ŀ����ͼ����֪OABC��һ�������Σ����ж���A��B������ֱ�Ϊ��0��a���ͣ�9��a������E��AB�ϣ���AE=AG����F��OC�ϣ���OF=![]() OC����G��OA�ϣ���ʹ��GEC�����Ϊ20����GFB�����Ϊ16������a��ֵ��
OC����G��OA�ϣ���ʹ��GEC�����Ϊ20����GFB�����Ϊ16������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ����ߵ��ұߵı����У��Ƿֽ���ʽ��Ϊ��������
A. a��x+y����ax+ay B. x2��4x+4��x��x��4��+4
C. x2��16+3x����x+4����x��4��+3x D. 10x2��5x��5x��2x��1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com