练习册

  • 练习册
  • 试题
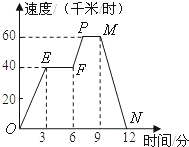
    精英家教网 > 初中数学 > 题目详情
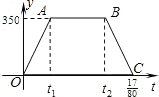    如图，图象（折线OEFPMN）描述了某汽车在行驶过程中速度与时间的函数关系．根据精英家教网图象所给的信息，下列说法中：
    ①第3分时汽车的速度是40千米/时；
    ②从第3分到第6分，汽车的速度是40千米/时；
    ③从第3分到第6分，汽车行驶了120千米；
    ④从第9分到第12分，汽车的速度从60千米/时减少到0千米/时；
    正确的有
     
    ．（只填序号）
    分析：依题意，根据图象可知，第3分汽车的速度为40千米/时，在第3分到第6分，汽车的速度是40千米/时，汽车行驶了2千米．从第9分到12分，汽车的速度从60千米/时逐渐变零．
    解答：解：从图中可获取的信息是：
    ①第3分时汽车的速度是40千米/时；
    ②从第3分到第6分，汽车的速度是40千米/时；
    ③从第3分到第6分，汽车行驶了40×
    3
    60
    =2千米；
    ④从第9分到第12分，汽车的速度从60千米/时减少到0千米/时．故错误的是③．故正确的有：①②④．
    点评：此题考查了学生从图象中读取信息的数形结合能力．解决此类识图题，同学们要注意分析其中的“关键点”，还要善于分析各图象的变化趋势．计算路程时，注意单位的统一．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网沪杭高速铁路已开工建设，某校研究性学习以此为课题，在研究列车的行驶速度时，得到一个数学问题．如图，若v是关于t的函数，图象为折线O-A-B-C，其中A（t1，350），B（t2，350），C（
    17
    80
    ，0），四边形OABC的面积为70，则t2-t1=（　　）
    A、
    1
    5
    B、
    3
    16
    C、
    7
    80
    D、
    31
    160

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    甲、乙、丙三人同时从A村出发去B村，刚开始甲骑自行车载乙，丙步行；a小时后甲骑车中途回头接丙，乙步行，结果三人同时到达B地．假设：乙、丙步行速度相同，甲载乙与甲载丙时速度相同，甲载人与不载人时的速度不同，甲、乙、丙三人与A村之间的距离y（千米）与出发的时间x（小时）之间的函数关系如图．（掉头与上下车时间忽略不计）
    精英家教网
    （1）选择：
    甲与A村之间的距离y（千米）与出发时间x（小时）之间的函数图象为折线（
     
    ）
    A、O-M-P     B、O-N-P     C、O-M-N-P     D、O-N-M-P
    乙与A村之间的距离y（千米）与出发时间x（小时）之间的函数图象为折线（
     
    ）
    A、O-M-P     B、O-N-P     C、O-M-N-P     D、O-N-M-P
    丙与A村之间的距离y（千米）与出发时间x（小时）之间的函数图象为折线（
     
    ）
    A、O-M-P     B、O-N-P     C、O-M-N-P     D、O-N-M-P
    （2）求步行速度，和甲载人骑车时的速度；
    （3）求a的值以及甲骑车走过的总路程．（写出必要的演算和推理过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

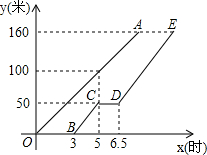    （2013•长春）甲、乙两工程队维修同一段路面，甲队先清理路面，乙队在甲队清理后铺设路面．乙队在中途停工了一段时间，然后按停工前的工作效率继续工作．在整个工作过程中，甲队清理完的路面长y（米）与时间x（时）的函数图象为线段OA，乙队铺设完的路面长y（米）与时间x（时）的函数图象为折线BC-CD-DE，如图所示，从甲队开始工作时计时．
    （1）分别求线段BC、DE所在直线对应的函数关系式．
    （2）当甲队清理完路面时，求乙队铺设完的路面长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某通信公司对移动电话有两种不同的收费方案．
    方案1：每分钟通话费0.2元；
    方案2：每分钟通话费0.3元，当每月通话时间超过某个时间后，超出部分的通话费打5折．
    如图是月通话费y（单位：元）与通话时间x（单位：分钟）的图象，其中射线OA是方案1的图象，折线OBC是方案2的图象，OA与BC相交于点P
    （1）根据图象，若通话100分钟，求两种方案的通话费分别是多少元？
    （2）根据图象，求方案2的通话费与通话时间之间的函数解析式；
    （3）现通信公司改进方案2的收费方式，统一为每分钟通话费0.15元，但需要交月租费，若通话300分钟时所交的总费用（月租费和通话费的总和）仅为60元，求月租费是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

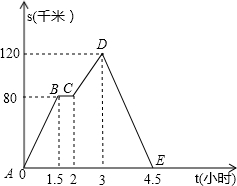    如图中的图象（折线ABCDE）描述了一汽车在某一直道上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系．根据图中提供的信息，给出下列说法：
    ①汽车共行驶了120千米；
    ②汽车在行驶途中停留了0.5小时；
    ③汽车在整个行驶过程中的平均速度为
    160
    3
    千米/时；
    ④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少．
    其中正确的说法有（　　）

    查看答案和解析>>

    同步练习册答案