
【题目】如图,在直角梯形ABCD中,AD∥BC,AD⊥DC,点A关于对角线BD的对称点F刚好落在腰DC上,连接AF交BD于点E,AF的延长线与BC的延长线交于点G,M,N分别是BG,DF的中点. 
(1)求证:四边形EMCN是矩形;
(2)若AD=2,S梯形ABCD= ![]() ,求矩形EMCN的长和宽.
,求矩形EMCN的长和宽.
【答案】
(1)证明:∵点A、F关于BD对称,
∴AD=DF,DE⊥AF,
又∵AD⊥DC,
∴△ADF、△DEF是等腰直角三角形,
∴∠DAF=∠EDF=45°,
∵AD∥BC,
∴∠G=∠GAD=45°,
∴△BGE是等腰直角三角形,
∵M,N分别是BG,DF的中点,
∴EM⊥BC,EN⊥CD,
又∵AD∥BC,AD⊥DC,
∴BC⊥CD,
∴四边形EMCN是矩形;
(2)解:由(1)可知,∠EDF=45°,BC⊥CD,
∴△BCD是等腰直角三角形,
∴BC=CD,
∴S梯形ABCD= ![]() (AD+BC)CD=
(AD+BC)CD= ![]() (2+CD)CD=
(2+CD)CD= ![]() ,
,
即CD2+2CD﹣15=0,
解得CD=3,CD=﹣5(舍去),
∵△ADE、△DEF是等腰直角三角形,
∴DF=AD=2,
∵N是DF的中点,
∴EN=DN= ![]() DF=
DF= ![]() ×2=1,
×2=1,
∴CN=CD﹣DN=3﹣1=2,
∴矩形EMCN的长和宽分别为2,1.
【解析】(1)根据轴对称的性质可得AD=DF,DE⊥AF,然后判断出△ADF、△DEF是等腰直角三角形,再根据等腰直角三角形的性质求出∠DAF=∠EDF=45°,根据两直线平行,内错角相等求出∠BGE=45°,然后判断出△BGE是等腰直角三角形,根据等腰直角三角形的性质可得EM⊥BC,EN⊥CD,再根据矩形的判定证明即可;(2)判断出△BCD是等腰直角三角形,然后根据梯形的面积求出CD的长,再根据等腰直角三角形的性质求出DN,即可得解.
【考点精析】关于本题考查的直角梯形,需要了解一腰垂直于底的梯形是直角梯形才能得出正确答案.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题:
甲组的5名工人9月份完成的总工作量比此月人均定额的4倍多30件,乙组的6名工人9月份完成的总工作量比此月人均定额的6倍少30件
(1)如果两组工人实际完成的此月人均工作量相等,那么此月人均定额是多少?
(2)如果甲组工人实际完成的此月人均工作量比乙组的多3件,则此月人均定额是多少?
(3)如果甲组工人实际完成的此月人均工作量比乙组的少3件,则此月人均定额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点, ![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC. 
(1)求证:AC是⊙O的切线:
(2)若BF=8,DF= ![]() ,求⊙O的半径r.
,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑摩托车从B地到A地,到达A地后立即按原路返回.如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
(1)直接写出y甲,y乙与x之间的函数关系式(不写过程);
(2)①求出点M的坐标,并解释该点坐标所表示的实际意义;
②根据图象判断,x取何值时,y乙>y甲.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据,估算袋中的白棋子数量为( )
A.60枚
B.50枚
C.40枚
D.30枚
查看答案和解析>>
科目:初中数学 来源: 题型:
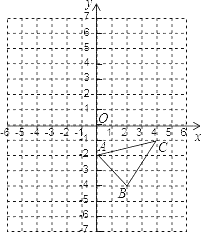
【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(a2-4a+2)(a2-4a+6)+4进行因式分解的过程:
解:设a2-4a=y,则
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(a2-4a+4)2.(第四步)
(1)该同学因式分解的结果是否彻底:________(填“彻底”或“不彻底”);
(2)若不彻底,请你直接写出因式分解的最后结果:________;
(3)请你模仿以上方法对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com