
����Ŀ���з��̽�Ӧ���⣺
�����5������9�·���ɵ��ܹ������ȴ����˾������4����30���������6������9�·���ɵ��ܹ������ȴ����˾������6����30��
��1��������鹤��ʵ����ɵĴ����˾���������ȣ���ô�����˾������Ƕ��٣�
��2��������鹤��ʵ����ɵĴ����˾�������������Ķ�3����������˾������Ƕ��٣�
��3��������鹤��ʵ����ɵĴ����˾����������������3����������˾������Ƕ��٣�
���𰸡���1�������˾�������55������2���������˾�������40������3�������˾�������70����
��������
������˾�����Ϊx�����������ܹ�����Ϊ��4x+30�������˾�Ϊ![]() ����������ܹ�����Ϊ��6x-30�����������˾�Ϊ��x-5������
����������ܹ�����Ϊ��6x-30�����������˾�Ϊ��x-5������
��1�����������˾���������ȣ����ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ�
��2�����ݼ�����˾��������������3�������ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ�
��3�����ݼ�����˾���������������3�������ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ�
�⣺������˾�����Ϊx�����������ܹ�����Ϊ��4x+30�������˾�Ϊ![]() ����������ܹ�����Ϊ��6x��30�����������˾�Ϊ��x��5������
����������ܹ�����Ϊ��6x��30�����������˾�Ϊ��x��5������
��1���������˾���������ȣ�
��![]() ��x��5��
��x��5��
��ã�x��55��
�𣺴����˾�������55����
��2��������˾��������������3����
��![]() ��3��x��5��
��3��x��5��
��ã�x��40��
�𣺴����˾�������40����
��3��������˾���������������3����
��![]() +3��x��5��
+3��x��5��
��ã�x��70��
�𣺴����˾�������70����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=�� ![]() x+3��x�ᡢy��ֱ���A��B���㣬��OΪ����ԭ�㣮
x+3��x�ᡢy��ֱ���A��B���㣬��OΪ����ԭ�㣮
��1�����ABO������ֵ��
��2�������A����ƽ��12����λ����C��ֱ��l����C����ֱ��y=�� ![]() x+3ƽ�У���ֱ��l�Ľ���ʽ��
x+3ƽ�У���ֱ��l�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʡij���ճ�Ϊȫ�˻������һ��ɱ�Ϊÿ��20Ԫ�Ĺ���Ʒ��Ͷ���г���������ÿ���������y���������ۼ�x��Ԫ/������һ�κ��������ۼ�Ϊ22Ԫ/��ʱ��ÿ��������Ϊ780�������ۼ�Ϊ25Ԫ/��ʱ��ÿ��������Ϊ750����
��1����y��x�ĺ�����ϵʽ��
��2������ù���Ʒ�ۼ���߲�����ÿ��30Ԫ����ô�ۼ۶�Ϊÿ������Ԫʱ�����ճ����۸ù���Ʒÿ���õ����������������Ƕ���Ԫ��������=�ۼ�-�ɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������رպϿ���S1 �� S2 �� S3 �� S4 �� S5�е��������ܹ�ʹ����L1 �� L2ͬʱ����ĸ����� �� 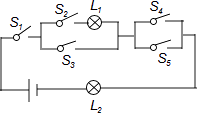
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P1��P2�Ƿ���������y= ![]() ��k��0���ڵ�һ����ͼ���ϵ����㣬��A1������Ϊ��4��0��������P1OA1���P2A1A2��Ϊ����ֱ�������Σ����е�P1��P2Ϊֱ�Ƕ��㣮
��k��0���ڵ�һ����ͼ���ϵ����㣬��A1������Ϊ��4��0��������P1OA1���P2A1A2��Ϊ����ֱ�������Σ����е�P1��P2Ϊֱ�Ƕ��㣮 
��1�����������Ľ���ʽ��
��2������P2�����꣮ �ڸ���ͼ��ֱ��д���ڵ�һ�����ڵ�x����ʲô����ʱ��������P1��P2��һ�κ����ĺ���ֵ���ڷ���������y= ![]() �ĺ���ֵ��
�ĺ���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC��ֱ�DZ�ABΪֱ������O����б��AC�ڵ�D����EΪOB���е㣬����CE���ӳ�����O�ڵ�F����Fǡ������ ![]() ���е㣬����AF���ӳ���CB���ӳ����ཻ�ڵ�G������OF��
���е㣬����AF���ӳ���CB���ӳ����ཻ�ڵ�G������OF�� 
��1����֤��OF= ![]() BG��
BG��
��2����AB=4����DC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ֱ������ϵ�У��������A��1��3������B��4��1������ֱ��д����A����x��ĶԳƵ�A1������A1 �� �� ��.
��2����x������һ��C��ʹAC+BC��ֵ��С�� ��������ͼ�ۼ�����
(3)�ó߹���x������һ��P��ʹPA=PB��������ͼ�ۼ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ɽ������һ����AB�����ײ�B�㵽ɽ��C��ľ���BCΪ6 ![]() �ף�ɽ�µ��½�Ϊ30�㣬С����ɽ�ŵ�ƽ��F������������ĸߣ���C�������EF��ˮƽ����CF=1�ף���E�����������A������Ϊ45�㣬���ײ�B������Ϊ20�㣬����AB�ĸ߶�.
�ף�ɽ�µ��½�Ϊ30�㣬С����ɽ�ŵ�ƽ��F������������ĸߣ���C�������EF��ˮƽ����CF=1�ף���E�����������A������Ϊ45�㣬���ײ�B������Ϊ20�㣬����AB�ĸ߶�.
���ο���ֵ��sin20���0.34��cos20���0.94��tan20���0.36��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABCD�У�AD��BC��AD��DC����A���ڶԽ���BD�ĶԳƵ�F�պ�������DC�ϣ�����AF��BD�ڵ�E��AF���ӳ�����BC���ӳ��߽��ڵ�G��M��N�ֱ���BG��DF���е㣮 
��1����֤���ı���EMCN�Ǿ��Σ�
��2����AD=2��S����ABCD= ![]() �������EMCN�ij��Ϳ���
�������EMCN�ij��Ϳ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com