
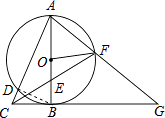
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在 ![]() 的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
的中点,连接AF并延长与CB的延长线相交于点G,连接OF. 
(1)求证:OF= ![]() BG;
BG;
(2)若AB=4,求DC的长.
【答案】
(1)证明:∵以Rt△ABC的直角边AB为直径作⊙O,点F恰好落在 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴∠AOF=∠BOF,
∵∠ABC=∠ABG=90°,
∴∠AOF=∠ABG,
∴FO∥BG,
∵AO=BO,
∴FO是△ABG的中位线,
∴FO= ![]() BG
BG
(2)解:在△FOE和△CBE中,
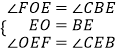 ,
,
∴△FOE≌△CBE(ASA),
∴BC=FO= ![]() AB=2,
AB=2,
∴AC= ![]() =2
=2 ![]() ,
,
连接DB,
∵AB为⊙O直径,
∴∠ADB=90°,
∴∠ADB=∠ABC,
∵∠BCD=∠ACB,
∴△BCD∽△ACB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:DC= ![]() .
.
【解析】(1)直接利用圆周角定理结合平行线的判定方法得出FO是△ABG的中位线,即可得出答案;(2)首先得出△FOE≌△CBE(ASA),则BC=FO= ![]() AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.


科目:初中数学 来源: 题型:
【题目】我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,点E是BD的中点,CE的延长线交边AB于点F,且∠CED=∠A. 
(1)求证:AC=AF;
(2)在边AB的下方画∠GBA=∠CED,交CF的延长线于点G,联结DG,在图中画出图形,并证明四边形CDGB是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
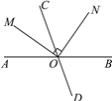
【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.
(1)若∠BOD=70°,求∠AOM和∠CON的度数;
(2)若∠BON=50°,求∠AOM和∠CON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
甲组的5名工人9月份完成的总工作量比此月人均定额的4倍多30件,乙组的6名工人9月份完成的总工作量比此月人均定额的6倍少30件
(1)如果两组工人实际完成的此月人均工作量相等,那么此月人均定额是多少?
(2)如果甲组工人实际完成的此月人均工作量比乙组的多3件,则此月人均定额是多少?
(3)如果甲组工人实际完成的此月人均工作量比乙组的少3件,则此月人均定额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax-2ax-3a(a<0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC交于点M,且PM= ![]() AB.
AB.
(1)求抛物线的解析式;
(2)点K是x轴正半轴上一点,点A、P关于点K的对称点分别为 ![]() 、
、 ![]() ,连接
,连接 ![]() 、
、 ![]() ,若
,若 ![]()
![]()
![]() ,求点K的坐标;
,求点K的坐标;
(3)矩形ADEF的边AF在x轴负半轴上,边AD在第二象限,AD=2,DE=3.将矩形ADEF沿x轴正方向平移t(t>0)个单位,直线AD、EF分别交抛物线于G、H.问:是否存在实数t,使得以点D、F、G、H为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的底边长为8cm,腰长为5cm,一动点P在底边上从B向C以0.25cm/s的速度移动,请你探究:当P运动几秒时,P点与顶点A的连线PA与腰垂直。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑摩托车从B地到A地,到达A地后立即按原路返回.如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
(1)直接写出y甲,y乙与x之间的函数关系式(不写过程);
(2)①求出点M的坐标,并解释该点坐标所表示的实际意义;
②根据图象判断,x取何值时,y乙>y甲.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com