
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��AOBΪ����A��B������ֱ�ΪA��0��4����B����3��0������Ҫ�����������⣮ 
��1������ͼ�У��Ƚ���AOB����ƽ��6����λ��������ƽ��3����λ������ƽ�ƺ�ġ�A1O1B1�������е�A��O��B�Ķ�Ӧ��ΪA1 �� O1 �� B1��
����ͼ�У�����A1O1B1�Ƶ�O1˳ʱ����ת90�㣬������ת���Rt��A2O1B2�������е�A1 �� B1�Ķ�Ӧ��ΪA2 �� B2��
��2��ֱ��д����A2 �� B2�����꣮

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD�У�E��F�ֱ���AB��AD���ϵĵ㣬DE��CF���ڵ�G��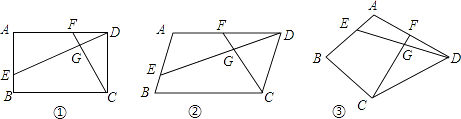
��1����ͼ�٣����ı���ABCD�Ǿ��Σ���DE��CF����֤����ADE�ס�DCF��
��2����ͼ�ڣ����ı���ABCD��ƽ���ı��Σ���̽��������B���EGC����ʲô��ϵʱ�� ![]() ��������֤����Ľ��ۣ�
��������֤����Ľ��ۣ�
��3����ͼ�ۣ���BA=BC=6��DA=DC=8����BAD=90�㣬DE��CF����ֱ��д�� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD���ĸ�����ȣ��ĸ���Ϊֱ�ǣ��У�E��F�ֱ�ΪAD��BC���е㣬PΪ�Խ���BD�ϵ�һ�����㣬�������߶εij�����AP+EP��Сֵ����( )
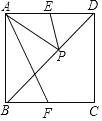
A. AB B. DE C. AF D. BD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��ABC��ֱ�������Σ���ACB=90�㣬��B��C���ڵ�һ�����ڣ�CA��x�ᣬ����Ϊ��A������������y1= ![]() ��ͼ����B������������y2=
��ͼ����B������������y2= ![]() ��ͼ����C��
��ͼ����C�� ![]() ��m����
��m����
��1�����B�����ꣻ
��2����ABC������Բ��M��BC��CA��AB�ֱ�������D��E��F����Բ��M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ڼ䣬ijѧУ�ƻ��ò�ɫ�ĵ���ש�����ѧ¥��ǰһ����βٳ�ABCD�ĵ��森��֪������βٳ�����ij�Ϊ100m����Ϊ80m��ͼ�������ͼ��ʾ���ٳ����Ľ�ΪС�����Σ���Ӱ����Ϊ�ĸ����Σ��ĸ����εĿ���ΪС�����εı߳�����ʵ������Ĺ����ܣ���Ӱ�����̺�ɫ����ש�����ಿ���̻�ɫ����ש�� 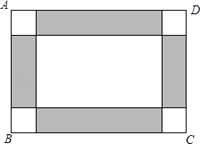
��1������ٳ����̻�ɫ����ש��������̺�ɫ����ש�����4������ô�ٳ��Ľǵ�ÿ��С�����α߳��Ƕ����ף�
��2�������ɫ����ש�ļ۸�Ϊÿƽ����30Ԫ����ɫ����ש�ļ۸�Ϊÿƽ����20Ԫ��ѧУ����15��Ԫ�ʽ�����Щ�ʽ��Ƿ��ܹ��������ȫ������ש������ܹ�����ѧ��ȫ������ש����ʣ���ʽ��Ƕ���Ԫ��������ܹ��������ȫ������ש�������ֻ�Ӧ�����ٸ�ѧУ��������ʽ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ڼ䣬ijѧУ�ƻ��ò�ɫ�ĵ���ש�����ѧ¥��ǰһ����βٳ�ABCD�ĵ��森��֪������βٳ�����ij�Ϊ100m����Ϊ80m��ͼ�������ͼ��ʾ���ٳ����Ľ�ΪС�����Σ���Ӱ����Ϊ�ĸ����Σ��ĸ����εĿ���ΪС�����εı߳�����ʵ������Ĺ����ܣ���Ӱ�����̺�ɫ����ש�����ಿ���̻�ɫ����ש�� 
��1������ٳ����̻�ɫ����ש��������̺�ɫ����ש�����4������ô�ٳ��Ľǵ�ÿ��С�����α߳��Ƕ����ף�
��2�������ɫ����ש�ļ۸�Ϊÿƽ����30Ԫ����ɫ����ש�ļ۸�Ϊÿƽ����20Ԫ��ѧУ����15��Ԫ�ʽ�����Щ�ʽ��Ƿ��ܹ��������ȫ������ש������ܹ�����ѧ��ȫ������ש����ʣ���ʽ��Ƕ���Ԫ��������ܹ��������ȫ������ש�������ֻ�Ӧ�����ٸ�ѧУ��������ʽ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DF��AB������ΪF��DE=DG����ADG�͡�AED������ֱ�Ϊ48��36�����EDF�����________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�߲˾�����ȥ�߲�������������ij���߲ˣ���֪�����߲˵���������20ǧ�ˡ�60ǧ��֮�䣨��20ǧ�˺�60ǧ�ˣ�ʱ��ÿǧ����������5Ԫ��������60ǧ��ʱ�������������߲�ȫ������ۣ��������ܽ�������300Ԫ��
��1���������⣬��д�����
�߲˵���������ǧ�ˣ� | �� | 25 | 60 | 75 | 90 | �� |
�����Ľ�Ԫ�� | �� | 125 | 300 | �� |
��2�������飬���߲˾��������۸����߲˵���������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ���һ�κ�����ϵ����ͼ����ͼ�����y��x֮��ĺ�����ϵʽ�� 
��3�������߲˾�����ÿ�����۴����߲˲�����75ǧ�ˣ��ҵ������ۼ۲��䣬��ô���ۼ۶�Ϊ����ʱ���þ��������۴����߲˵ĵ�����������������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AD��BC��E��F����ֱ���AB��AD�ϣ�CE��BF�ཻ��G�㣮����EBG=25�㣬��GCB=20�㣬��AEG=95�㣬���A�Ķ���Ϊ�Σ��������� 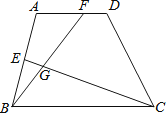
A.95
B.100
C.105
D.110
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com