
����Ŀ������ڼ䣬ijѧУ�ƻ��ò�ɫ�ĵ���ש�����ѧ¥��ǰһ����βٳ�ABCD�ĵ��森��֪������βٳ�����ij�Ϊ100m����Ϊ80m��ͼ�������ͼ��ʾ���ٳ����Ľ�ΪС�����Σ���Ӱ����Ϊ�ĸ����Σ��ĸ����εĿ���ΪС�����εı߳�����ʵ������Ĺ����ܣ���Ӱ�����̺�ɫ����ש�����ಿ���̻�ɫ����ש�� 
��1������ٳ����̻�ɫ����ש��������̺�ɫ����ש�����4������ô�ٳ��Ľǵ�ÿ��С�����α߳��Ƕ����ף�
��2�������ɫ����ש�ļ۸�Ϊÿƽ����30Ԫ����ɫ����ש�ļ۸�Ϊÿƽ����20Ԫ��ѧУ����15��Ԫ�ʽ�����Щ�ʽ��Ƿ��ܹ��������ȫ������ש������ܹ�����ѧ��ȫ������ש����ʣ���ʽ��Ƕ���Ԫ��������ܹ��������ȫ������ש�������ֻ�Ӧ�����ٸ�ѧУ��������ʽ�
���𰸡�
��1���⣺��ٳ��Ľǵ�ÿ��С�����α߳���x�ף��������⣬
�ã�4x2+��100��2x����80��2x��=4[2x��100��2x��+2x��80��2x��]��
�������ã�x2��45x+200=0��
��ã�x1=5��x2=40����ȥ����
�ʲٳ��Ľǵ�ÿ��С�����α߳���5��
��2���⣺���̾��ι㳡������ܷ���ΪyԪ���㳡�Ľǵ�С�����εı߳�Ϊx�ף�
��y=30��[4x2+��100��2x����80��2x��]+20��[2x��100��2x��+2x��80��2x��]
����y=80x2��3600x+240000
�䷽�ã�y=80��x��22.5��2+199500
��x=22.5ʱ��y��ֵ��С����СֵΪ19.95��Ԫ��15��Ԫ��
����Щ�ʽ��ܹ��������ȫ������ש�������ֻ�Ӧ�����ٸ�ѧУ���19.95��15=4.95��Ԫ�ʽ�
����������1����С�����εı߳�Ϊx�ף���ʾ����ߴ���εij�Ϊ��100��2x���ף���Ϊ��80��2x���ף����û�ɫ���ֵ����=4��С�����ε����+��ߴ���ε��������ɫ�������=���������������+��������������������ݻ�ɫ����ש��������̺�ɫ����ש�����4���г�����x�ķ��̣�������̵Ľ�õ�x��ֵ����ΪС�����εı߳�����2�����̾��ι㳡������ܷ���ΪyԪ���㳡�Ľǵ�С�����εı߳�Ϊx�ף����ݵ�����ϵ���ܷ���=�̰�ɫ����ש�ķ���+����ɫ����ש�ķ��á��г�y����x�ĺ����������Сֵ����15��Ԫ�ȽϿɵ��Ƿ��ã�


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������վ���㳡����2015���Ͷ��ʹ�ã��ƻ��ڹ㳡����ֲA��B���ֻ�ľ��6600�ã���A��ľ������B��ľ������2����600��
��1��A��B���ֻ�ľ�������ֱ��Ƕ��ٿã�
��2������ִ�����26��ͬʱ��ֲ�����ֻ�ľ��ÿ��ÿ������ֲA��ľ60�û�B��ľ40�ã�Ӧ�ֱ��Ŷ�������ֲA��ľ��B��ľ������ȷ��ͬʱ��ɸ��Ե�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Сǿ����ö�ʵؾ��ȵ����ӣ�ÿ�����ӵ��������Ϸֱ����1��6�ĵ���������ö���ӵ�����ͬ�ĸ���Ϊ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y=![]() ��x���ڵ�A����y���ڵ�B����A1��A2��A3������x���ϣ���B1��B2��B3������ֱ��l�ϣ�����OB1A����A1B2A2����A2B3A3������Ϊ�ȱ������Σ�����A5B6A6�������__��
��x���ڵ�A����y���ڵ�B����A1��A2��A3������x���ϣ���B1��B2��B3������ֱ��l�ϣ�����OB1A����A1B2A2����A2B3A3������Ϊ�ȱ������Σ�����A5B6A6�������__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��AOBΪ����A��B������ֱ�ΪA��0��4����B����3��0������Ҫ�����������⣮ 
��1������ͼ�У��Ƚ���AOB����ƽ��6����λ��������ƽ��3����λ������ƽ�ƺ�ġ�A1O1B1�������е�A��O��B�Ķ�Ӧ��ΪA1 �� O1 �� B1��
����ͼ�У�����A1O1B1�Ƶ�O1˳ʱ����ת90�㣬������ת���Rt��A2O1B2�������е�A1 �� B1�Ķ�Ӧ��ΪA2 �� B2��
��2��ֱ��д����A2 �� B2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC���������������ֱ�Ϊ��A����2��3����B����6��0����C����1��0���� 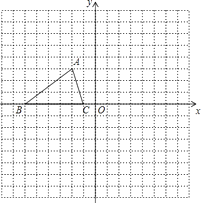
��1������ABC��y�ᷭ�ۣ��������ۺ�ġ�A1B1C1 �� ��A�Ķ�Ӧ��A1��������
��2����ABC����x��ԳƵ�ͼ�Ρ�A2B2C2 �� ֱ��д����A2������
��3������DBC���ABCȫ�ȣ���D���A�غϳ��⣩����ֱ��д������������D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC��AD��BC��CE��AB��AE=CE����֤�� 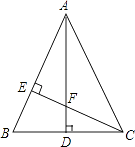
��1����AEF�ա�CEB��
��2��AF=2CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ֱ��������ֽƬABO��������ƽ��ֱ������ϵ�У���A�� ![]() ��0������B��0��1������0��0��0��������OA�ϵĶ���M����M�����O��A�غϣ���MN�AAB�ڵ�N������MN�۵���ֽƬ���ö���A�Ķ�Ӧ��A�䣬��OM=m���۵���ġ�AM��N���ı���OMNB�ص����ֵ����ΪS��
��0������B��0��1������0��0��0��������OA�ϵĶ���M����M�����O��A�غϣ���MN�AAB�ڵ�N������MN�۵���ֽƬ���ö���A�Ķ�Ӧ��A�䣬��OM=m���۵���ġ�AM��N���ı���OMNB�ص����ֵ����ΪS��
��1����ͼ�٣�����A���붥��B�غ�ʱ�����M�����ꣻ
��2����ͼ�ڣ�����A�䣬���ڵڶ�����ʱ��A��M��OB�ཻ�ڵ�C�����ú�m��ʽ�ӱ�ʾS��
��3����S= ![]() ʱ�����M�����ֱ꣨��д��������ɣ���
ʱ�����M�����ֱ꣨��д��������ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס����������ò�ͬ�Ľ�ͨ���ߣ���ͬһ·�ߴ�A�س���ǰ��B�أ��׳���1h���ҳ����������A�����y����km��������A�����y����km�������뿪A��ʱ��Ϊx��h����y����y����x֮��ĺ���ͼ����ͼ��ʾ��
��1�����ٶ����� ��km/h��
��2����ֱ����y����y����x֮��ĺ�����ϵʽ��
��3��������A�����240kmʱ������B��������ǧ�ף�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com