
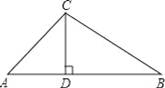
如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=1,则AB的长为 .

1+
 .
.
【考点】解直角三角形.
【专题】计算题.
【分析】在直角三角形BCD中,利用30度角所对的直角边等于斜边的一半,根据CD的长求出BC的长,利用勾股定理求出BD的长,在直角三角形ACD中,根据∠A的度数确定出此三角形为等腰直角三角形,得出AD=CD=1,由AD+DB即可求出AB的长.
【解答】解:在Rt△BCD中,∠B=30°,CD=1,
∴BC=2CD=2,
根据勾股定理得:BD=
 =
=
 ,
,
在Rt△ACD中,∠A=45°,CD=1,
∴AD=CD=1,
则AB=AD+DB=1+
 .
.
故答案为:1+
 .
.
【点评】此题考查了解直角三角形,涉及的知识有:勾股定理,锐角三角函数定义,含30度直角三角形的性质,熟练掌握勾股定理是解本题的关键.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
某物质的密度ρ(kg/m3)关于其体积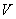 (m3)的函数图像如图所示,那么ρ与
(m3)的函数图像如图所示,那么ρ与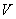 之间的函数表达式是 ( )
之间的函数表达式是 ( )
A. ρ=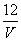 B. ρ=
B. ρ=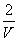 C. ρ=
C. ρ=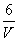 D.
D. 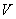 ρ=3
ρ=3
|
第2题 第4题 第5题 第7题 第8题
查看答案和解析>>
科目:初中数学 来源: 题型:
我们学过反比例函数,例如,当矩形面积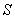 一定时,长
一定时,长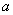 是宽
是宽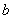 的反比例函数,其函数表达式可以写成
的反比例函数,其函数表达式可以写成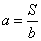 (
(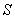 为常数,
为常数,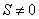 ).请你仿照上例另举出一个在日常生活、生产或学习中具有反比例函数关系的实例,并写出它的函数表达式.
).请你仿照上例另举出一个在日常生活、生产或学习中具有反比例函数关系的实例,并写出它的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若 °,则∠BFC的大小是( )°.(用含x的式子表示)
°,则∠BFC的大小是( )°.(用含x的式子表示)
A. x B. 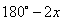 C. 180°-x D.2x
C. 180°-x D.2x

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com