
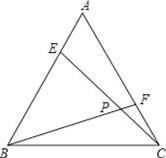
如图,E、F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE、BF交于点P.
(1)求证:CE=BF;
(2)求∠BPC的度数.

【考点】全等三角形的判定与性质;等边三角形的性质.
【分析】(1)欲证明CE=BF,只需证得△BCE≌△ABF;
(2)利用(1)中的全等三角形的性质得到∠BCE=∠ABF,则由图示知∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°,即∠PBC+∠PCB=60°,所以根据三角形内角和定理求得∠BPC=120°.
【解答】(1)证明:如图,∵△ABC是等边三角形,
∴BC=AB,∠A=∠EBC=60°,
∴在△BCE与△ABF中,
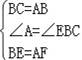
 ,
,
∴△BCE≌△ABF(SAS),
∴CE=BF;
(2)解:∵由(1)知△BCE≌△ABF,
∴∠BCE=∠ABF,
∴∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°,即∠PBC+∠PCB=60°,
∴∠BPC=180°﹣60°=120°.
即:∠BPC=120°.
【点评】本题考查了全等三角形的判定与性质、等边三角形的性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.


科目:初中数学 来源: 题型:
如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B、C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依此操作下去…
(1)图2中的△EFD是经过两次操作后得到的,其形状为 ,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 ,此时AE与BF的数量关系是 ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
)如图①,小华设计了一个探究杠杆平衡条件的实验:在一根质地均匀的木杆中点 的左侧固定位置
的左侧固定位置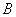 处悬挂重物
处悬挂重物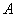 ,在中点
,在中点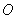 的右侧用一个弹簧秤向下拉,改变弹簧秤与点
的右侧用一个弹簧秤向下拉,改变弹簧秤与点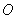 的距离
的距离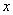 (cm),观察弹簧秤的示数
(cm),观察弹簧秤的示数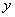 (N)的变化情况.实验数据记录如下表:
(N)的变化情况.实验数据记录如下表:
|
| … | 10 | 15 | 20 | 25 | 30 | … |
|
| … | 30 | 20 | 15 | 12 | 10 | … |
|
第24题
(1)把上表中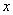 、
、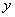 的各组对应值作为点的坐标,在平面直角坐标系中(如图②所示)描出相应的点,用平滑的曲线连接这些点并观察所得到的图像,猜测
的各组对应值作为点的坐标,在平面直角坐标系中(如图②所示)描出相应的点,用平滑的曲线连接这些点并观察所得到的图像,猜测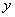 (N)与
(N)与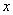 (cm)之间的函数关系,并求出函数表达式.
(cm)之间的函数关系,并求出函数表达式.
(2)当弹簧秤的示数为24N时,求弹簧秤与点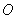 的距离.随着弹簧秤与点
的距离.随着弹簧秤与点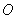 的距离不断减小,弹簧秤上的示数将发生怎样的变化?
的距离不断减小,弹簧秤上的示数将发生怎样的变化?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com