练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．一元二次方程2（5x+1）2=3（1+5x）的根为x1=-$\frac{1}{5}$，x2=$\frac{1}{10}$．

    分析 移项后分解因式，即可得出两个一元一次方程，求出方程的解即可．

    解答 解：2（5x+1）2=3（1+5x）
    2（5x+1）2-3（1+5x）=0，
    （5x+1）[2（5x+1）-3]=0，
    5x+1=0，2（5x+1）-3=0，
    x1=-$\frac{1}{5}$，x2=$\frac{1}{10}$
    故答案为x1=-$\frac{1}{5}$，x2=$\frac{1}{10}$．

    点评 本题考查了解一元二次方程的应用，解此题的关键是能选择适当的方法解一元二次方程，题目比较好，难度适中．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

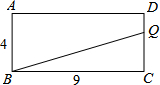    11．如图，长方形ABCD中，AB=4，BC=9，动点Q沿着C→D→A→B的方向运动至点B停止，设点Q运动的路程为x，△QCB的面积为y．
    （1）当点Q在CD上运动时，求y与x的关系式；
    （2）当点Q在AD上运动时，△QCB的面积是否发生变化，请说明理由；
    （3）当点Q运动到AB上时，△QCB的面积是否发生变化，如果发生变化求出面积变化范围，并写出y与x的关系式，如果没有发生变化，求出此时△QCB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．计算：$\frac{2m}{n}$•$\frac{{n}^{2}}{4{m}^{2}}$=$\frac{n}{2m}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．对于命题“如果∠1+∠2=90°，那么∠1=∠2”，能说明它是假命题的反例是（　　）
    A．∠1=45°，∠2=45°B．∠1=50°，∠2=50°C．∠1=50°，∠2=40°D．∠1=40°，∠2=40°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知，如图，在四边形ABCD中，AC、BD交于点O，AD∥BC，请你添加一个条件（不再添加其他线段，不再标注或使用其他字母），使AB=CD；并给出证明．
    你添加的一个条件是：AD=CB
    证明：

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图，将边长为4的正方形ABCD沿其对角线AC剪开，固定△ADC，并把△ABC沿着AD方向平移，得到△A′B′C′，当两个三角形重叠部分的面积为2时，它移动的距离AA′等于2+$\sqrt{2}$或2-$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．-2014的相反数是2014，$-\frac{1}{3}$的倒数为-3，-35的绝对值等于35．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．大家知道|5|=|5-0|，它在数轴上的意义是表示5的点与原点（即表示0的点）之间的距离．又如式子|6-3|，它在数轴上的意义是表示6的点与表示3的点之间的距离．即点A、B在数轴上分别表示数a、b，则A、B两点的距离可表示为：|AB|=|a-b|．根据以上信息，回答下列问题：
    （1）数轴上表示2和5的两点之间的距离是1；数轴上表示-3和15的两点之间的距离是1；
    （2）点A、B在数轴上分别表示数x和-1．
    ①用代数式表示A、B两点之间的距离；
    ②如果|AB|=2，求x值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．矩形有而平行四边形没有的性质是（　　）
    A．对角相等B．对边相等C．邻角互补D．对角线相等

    查看答案和解析>>

    同步练习册答案