Question

如图，已知在Rt△ABC中，∠ABC=90°，∠C=30°，AC=12cm，点E从点A出发沿AB以每秒1cm的速度向点B运动，同时点D从点C出发沿CA以每秒2cm的速度向点A运动，运动时间为t秒（0<t<6），过点D作DF⊥BC于点F．

（1）如图①，在D、E运动的过程中，四边形AEFD是平行四边形，请说明理由；

（2）连接DE，当t为何值时，△DEF为直角三角形？

（3）如图②，将△ADE沿DE翻折得到△A′DE，试问当t为何值时，四边形 AEA′D为菱形？

 

Answer 1

【答案】

（1）先根据含30°角的直角三角形的性质可得DF=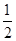CD=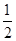×2t=t，即可得到DF="AE" ，由∠ABC=90°，DF⊥BC可得DF∥AE，即可证得结论；（2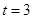）秒或秒；（3）4

【解析】

试题分析：（1）先根据含30°角的直角三角形的性质可得DF=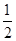CD=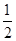×2t=t，即可得到DF="AE" ，由∠ABC=90°，DF⊥BC可得DF∥AE，即可证得结论；

（2）①显然∠DFE < 90°，②当∠EDF=90°时，四边形EBFD为矩形，③当∠DEF=90°时，此时∠ADE = 90°，分这三种情况根据直角三角形、矩形的性质求解即可；

（3）根据菱形的性质可得AE=AD，即可得到关于t的方程，再解出即可.

（1）∵DF⊥BC，∠C=30°

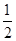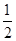∴DF=CD=×2t=t

∵AE=t

∴DF="AE"

∵∠ABC=90°，DF⊥BC

∴DF∥AE  

∴四边形AEFD是平行四边形；

（2）①显然 ∠DFE < 90°

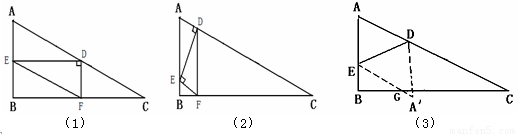
②如图（1），当∠EDF = 90°时，四边形EBFD为矩形，

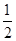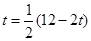此时AE=AD，即，解得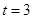

③如图（2），当∠DEF = 90°时，此时∠ADE = 90°

∴∠AED = 90°－∠A=30°

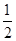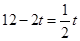∴AD=AE，即，解得

综上：当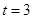秒或秒时，⊿DEF为直角三角形；

（3）如图（3），若四边形AEA′D为菱形，则AE=AD

∴t=12－2t，解得t=4

∴当t=4时，四边形AEA′D为菱形.

考点：动点问题的综合题

点评：此类问题难度较大，在中考中比较常见，一般在压轴题中出现，需特别注意.