

���� ��1���������ı���ȵ��ı����������жϼ��ɣ�
�������S��OAB=$\frac{1}{2}$OB��AE=10���������AE�����ɵó���A�����ꣻ�����ù��ɶ������ɵó����ۣ�
��2�������жϳ���AOB�ǵȱ������Σ����õȱ������ε����ʼ��������A�����꣬
�ڹ����ֱ�������Σ����âٵĽ��۵ó���B'AF=30�㣬�������AF��B'F���ɵó����ۣ�
��� �⣺��1���١ߵ�D��AB�е㣬
��AD=BD��
����ת�ã�BC=OA��AC=OB��
��OA=OB��
��OA=OB=BC=AC��
���ı���OACB�����Σ�
������ת֪����ABC�ա�BOA��
��S��ABC=S��BOA��
���ı���OACB�����Ϊ20��
��S��OAB=$\frac{1}{2}$OB��AE=10��
��B��5��0����
��OB=5��
��AE=4��
���ݹ��ɶ����ã�OE=3��
��A��3��4����
��D��4��2����
��ֱ��OC�Ľ���ʽΪy=$\frac{1}{2}$x��
��F��3��$\frac{3}{2}$����
��OF=$\sqrt{9+\frac{9}{4}}$=$\frac{3\sqrt{5}}{2}$��
���ı���OACB�����Σ���A��3��4����B��5��0����
��C��8��4����
��OC=$\sqrt{64+16}$=4$\sqrt{5}$��
��CF=OC-OF=$\frac{5\sqrt{5}}{2}$��
��2������ͼ��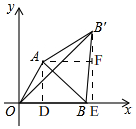 ����A��AD��OB��
����A��AD��OB��
��OA=OB=5����AOB=60�㣬
���AOB�ǵȱ������Σ�
��AB=OB=5��OD=$\frac{5}{2}$��AD=$\frac{5}{2}\sqrt{3}$��
��A��$\frac{5}{2}$��$\frac{5}{2}\sqrt{3}$����
���ɢ�֪��A��$\frac{5}{2}$��$\frac{5}{2}\sqrt{3}$����
��B'��B'E��OB������A��AF��B'E��
���DAF=��AFB'=90�㣬
�ߡ�OAB��A��ת90���ʱ��B��B��λ�ã�
��AB=AB'����BAB'=90�㣬
���OAB'=150�㣬
���B'AF=30�㣬
��Rt��AB'F��AB'=AB=5��
��B'F=$\frac{5}{2}$��AF=$\frac{5}{2}\sqrt{3}$��
��OE=OD+AF=$\frac{5}{2}$+$\frac{5}{2}\sqrt{3}$��B'E=B'F+AD=$\frac{5}{2}$+$\frac{5}{2}\sqrt{3}$��
��B'��$\frac{5}{2}$+$\frac{5}{2}\sqrt{3}$��$\frac{5}{2}$+$\frac{5}{2}\sqrt{3}$����
���� �����Ǽ��α任�ۺ��⣬��Ҫ���������ε��ж������ʣ������ε������ʽ�����ɶ�������30��ǵ�ֱ�������ε����ʣ��ȱ������ε��ж������ʣ��Ȿ��Ĺؼ��ǹ����ֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{5}$ | B�� | 5 | C�� | $\frac{\sqrt{5}}{5}$ | D�� | $\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | -2 | C�� | -1��2 | D�� | -1��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��֪��ͼ����C���߶�AB�Ļƽ�ָ�㣨AC��BC���������н�������ȷ���ǣ�������
��֪��ͼ����C���߶�AB�Ļƽ�ָ�㣨AC��BC���������н�������ȷ���ǣ�������| A�� | AB2=AC2+BC2 | B�� | BC2=AC•BA | C�� | AC2=AB•BC | D�� | AC=2BC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com