
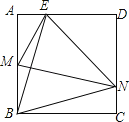
【题目】如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )
A.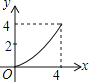
B.
C.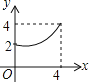
D.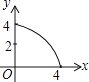
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请找出截面的圆心;(不写画法,保留作图痕迹.)
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(﹣1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )

A.8:1
B.6:1
C.5:1
D.4:1
查看答案和解析>>
科目:初中数学 来源: 题型:
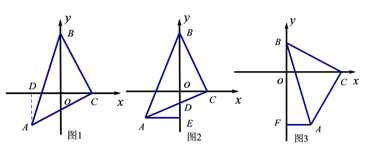
【题目】如图所示:△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一锐角顶点B在y轴上.
(1)如图1所示,若C的坐标是(2,0),点A的坐标是(﹣2,﹣2),求:点B的坐标;
(思路提示:过点A作AD⊥x轴于点D,通过证明△BOC≌△CDA来达到目的.)
(2)如图2,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴 于E,问BD与AE有怎样的数量关系,并说明理由;
(3)如图3,直角边BC的两个端点在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,两个结论①![]() 为定值;②
为定值;②![]() 为定值,只有一个结论成立,请你判断正确的结论加以证明,并求出定值.
为定值,只有一个结论成立,请你判断正确的结论加以证明,并求出定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),将两块直角三角板的直角顶点C叠放在一起. 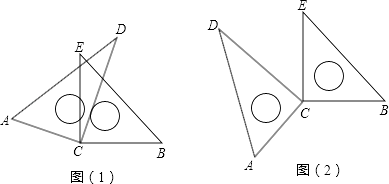
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
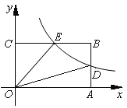
【题目】如图,在以O为原点的直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B(a,b)在第一象限,四边形OABC是矩形,若反比例函数![]() (k>0,x>0)的图象与AB相交于点D,与BC相交于点E,且BE=CE.
(k>0,x>0)的图象与AB相交于点D,与BC相交于点E,且BE=CE.
(1)求证:BD=AD;
(2)若四边形ODBE的面积是9,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com