
ЁОЬтФПЁПШчЭМЫљЪОЃКЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌBC=ACЃЌжБНЧЖЅЕуCдкxжсЩЯЃЌвЛШёНЧЖЅЕуBдкyжсЩЯ.
ЃЈ1ЃЉШчЭМ1ЫљЪОЃЌШєCЕФзјБъЪЧЃЈ2ЃЌ0ЃЉЃЌЕуAЕФзјБъЪЧЃЈЉ2ЃЌЉ2ЃЉЃЌЧѓЃКЕуBЕФзјБъЃЛ
ЃЈЫМТЗЬсЪОЃКЙ§ЕуAзїADЁЭxжсгкЕуDЃЌЭЈЙ§жЄУїЁїBOCЁеЁїCDAРДДяЕНФПЕФ.ЃЉ
ЃЈ2ЃЉШчЭМ2ЃЌШєyжсЧЁКУЦНЗжЁЯABCЃЌACгыyжсНЛгкЕуDЃЌЙ§ЕуAзїAEЁЭyжс гкEЃЌЮЪBDгыAEгадѕбљЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌжБНЧБпBCЕФСНИіЖЫЕудкСНзјБъжсЩЯЛЌЖЏЃЌЪЙЕуAдкЕкЫФЯѓЯоФкЃЌЙ§AЕузїAFЁЭyжсгкFЃЌдкЛЌЖЏЕФЙ§ГЬжаЃЌСНИіНсТлЂй![]() ЮЊЖЈжЕЃЛЂк
ЮЊЖЈжЕЃЛЂк![]() ЮЊЖЈжЕЃЌжЛгавЛИіНсТлГЩСЂЃЌЧыФуХаЖЯе§ШЗЕФНсТлМгвджЄУїЃЌВЂЧѓГіЖЈжЕЃЎ
ЮЊЖЈжЕЃЌжЛгавЛИіНсТлГЩСЂЃЌЧыФуХаЖЯе§ШЗЕФНсТлМгвджЄУїЃЌВЂЧѓГіЖЈжЕЃЎ
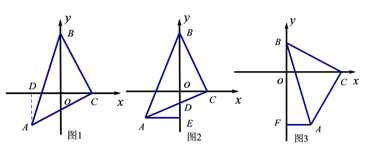
ЁОД№АИЁП(1) ЃЈ0ЃЌ4ЃЉЃЛ(2) BD=2AE,РэгЩМћНтЮіЃЛЃЈ3ЃЉ1
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЙ§ЕуAзїADЁЭxжсЃЌПЩжЄЁїADCЁеЁїCOBЃЌИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШМДПЩНтЬтЃЛЃЈ2ЃЉбгГЄBCЃЌAEНЛгкЕуFЃЌПЩжЄЁїACFЁеЁїBCDЃЌЁїABEЁеЁїFBEЃЌМДПЩЧѓЕУBD=2AEЃЛ
ЃЈ3ЃЉзїAEЁЭOCЃЌдђAF=OEЃЌПЩжЄЁїBCOЁеЁїACEЃЌПЩЕУAF+OB=OCЃЌМДПЩНтЬтЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉЙ§ЕуAзїADЁЭxжсЃЌ
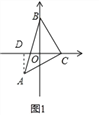
ЁпЁЯDAC+ЁЯACD=90ЁуЃЌЁЯACD+ЁЯBCD=90ЁуЃЌ
ЁрЁЯBCD=ЁЯDACЃЌ
дкЁїADCКЭЁїCOBжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїADCЁеЁїCOBЃЈAASЃЉЃЌ
ЁрAD=OCЃЌCD=OBЃЌ
ЁрЕуBзјБъЮЊЃЈ0ЃЌ4ЃЉЃЛ
ЃЈ2ЃЉбгГЄBCЃЌAEНЛгкЕуFЃЌ
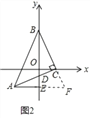
ЁпAC=BCЃЌACЁЭBCЃЌ
ЁрЁЯBAC=ЁЯABC=45ЁуЃЌ
ЁпBDЦНЗжЁЯABCЃЌ
ЁрЁЯCOD=22.5ЁуЃЌЁЯDAE=90ЁуЉЁЯABDЉЁЯBAD=22.5ЁуЃЌ
дкЁїACFКЭЁїBCDжаЃЌ
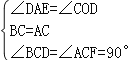 ЃЌ
ЃЌ
ЁрЁїACFЁеЁїBCDЃЈASAЃЉЃЌ
ЁрAF=BDЃЌ
дкЁїABEКЭЁїFBEжаЃЌ
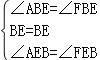 ЃЌ
ЃЌ
ЁрЁїABEЁеЁїFBEЃЈASAЃЉЃЌ
ЁрAE=EFЃЌ ЁрBD=2AEЃЛ
ЃЈ3ЃЉзїAEЁЭOCЃЌдђAF=OEЃЌ
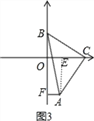
ЁпЁЯCBO+ЁЯOBC=90ЁуЃЌЁЯOBC+ЁЯACO=90ЁуЃЌ
ЁрЁЯACO=ЁЯCBOЃЌ
дкЁїBCOКЭЁїACEжаЃЌ
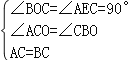 ЃЌ
ЃЌ
ЁрЁїBCOЁеЁїACEЃЈAASЃЉЃЌ ЁрCE=OBЃЌ ЁрOB+AF=OCЃЎ
Ёр![]() =1ЃЎ
=1ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУЙЋЪНЗЈНтЗНГЬ5x2=6x-8ЪБЃЌaЁЂbЁЂcЕФжЕЗжБ№ЪЧЃЈЁЁЁЁЃЉ
A.5ЁЂ6ЁЂ-8
B.5ЁЂ-6ЁЂ-8
C.5ЁЂ-6ЁЂ8
D.6ЁЂ5ЁЂ-8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
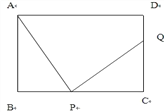
ЁОЬтФПЁПШчЭМЃЌдкГЄЗНаЮABCDжаЃЌAB=CD=6cmЃЌBC=10cm,ЕуPДгЕуBГіЗЂЃЌвд2cm/УыЕФЫйЖШбиBCЯђЕуCдЫЖЏЁЃЩшЕуPЕФдЫЖЏЪБМфЮЊtУы,ЕБЕуPДгЕуBПЊЪМдЫЖЏЃЌЭЌЪБЃЌЕуQДгЕуCГіЗЂЃЌбиCDЯђЕуDдЫЖЏЃЌЕБt =________УыЪБЃЌвдPЁЂCЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїABPШЋЕШЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЮЊе§ЗНаЮЃЌШєAB=4ЃЌEЪЧADБпЩЯвЛЕуЃЈЕуEгыЕуAЁЂDВЛжиКЯЃЉЃЌBEЕФжаДЙЯпНЛABгкЕуMЃЌНЛDCгкЕуNЃЌЩшAE=xЃЌBM=yЃЌдђyгыxЕФДѓжТЭМЯѓЪЧЃЈ ЃЉ
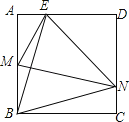
A.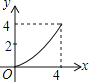
B.
C.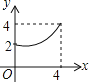
D.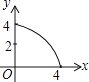
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌCЮЊЩфЯпABЩЯвЛЕуЃЌAB=30ЃЌACБШBCЕФ ![]() Жр5ЃЌPЃЌQСНЕуЗжБ№ДгAЃЌBСНЕуЭЌЪБГіЗЂЃЎЗжБ№вд2ЕЅЮЛ/УыКЭ1ЕЅЮЛ/УыЕФЫйЖШдкЩфЯпABЩЯбиABЗНЯђдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЌMЮЊBPЕФжаЕуЃЌNЮЊQMЕФжаЕуЃЌвдЯТНсТлЃК ЂйBC=2ACЃЛЂкAB=4NQЃЛЂлЕБPB=
Жр5ЃЌPЃЌQСНЕуЗжБ№ДгAЃЌBСНЕуЭЌЪБГіЗЂЃЎЗжБ№вд2ЕЅЮЛ/УыКЭ1ЕЅЮЛ/УыЕФЫйЖШдкЩфЯпABЩЯбиABЗНЯђдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЌMЮЊBPЕФжаЕуЃЌNЮЊQMЕФжаЕуЃЌвдЯТНсТлЃК ЂйBC=2ACЃЛЂкAB=4NQЃЛЂлЕБPB= ![]() BQЪБЃЌt=12ЃЌЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
BQЪБЃЌt=12ЃЌЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ![]()
A.0
B.1
C.2
D.3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛЬѕжБЯпЩЯШЮШЁвЛЕуAЃЌНиШЁAB=20cmЃЌдйНиШЁAC=18cmЃЌMЁЂNЗжБ№ЪЧABЁЂACЕФжаЕуЃЌдђMЁЂNСНЕужЎМфЕФОрРыЮЊcmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСагяОфВЛЪЧУќЬтЕФЪЧЃЈ ЃЉ
A. ЖдЖЅНЧЯрЕШ B. СЌНгABВЂбгГЄжСCЕу
C. ФкДэНЧЯрЕШ D. ЭЌНЧЕФгрНЧЯрЕШ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЫвЧБЫЎЭЇЫљдкЕФКЃАЮИпЖШЮЊЉ50mЃЌШєвЛЬѕішгудкЧБЫЎЭЇЯТЗН10mДІЃЌдђішгуЫљдкЕФКЃАЮИпЖШЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаетбљвЛЕРЬтЃКЁАМЦЫуЃЈ2x3Љ3x2yЉ2xy2ЃЉЉЃЈx3Љ2xy2+y3ЃЉ+ЃЈЉx3+3x2yЉy3ЃЉЕФжЕЃЌЦфжа ![]() ЁБЃЎМзЭЌбЇАбЁА
ЁБЃЎМзЭЌбЇАбЁА ![]() ЁБДэГГЩЁА
ЁБДэГГЩЁА ![]() ЁБЃЌЕЋЫћМЦЫуЕФНсЙћвВЪЧе§ШЗЕФЃЌЪдЫЕУїРэгЩЃЌВЂЧѓГіетИіНсЙћЃЎ
ЁБЃЌЕЋЫћМЦЫуЕФНсЙћвВЪЧе§ШЗЕФЃЌЪдЫЕУїРэгЩЃЌВЂЧѓГіетИіНсЙћЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com