
【题目】如图∠A=∠ABC=∠C=45°,E、F分别是AB、BC的中点,则下列结论,①EF⊥BD,②EF=![]() BD,③∠ADC=∠BEF+∠BFE,④AD=DC,其中正确的是( )
BD,③∠ADC=∠BEF+∠BFE,④AD=DC,其中正确的是( )
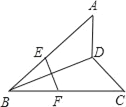
A. ①②③④ B. ①②③ C. ①②④ D. ②③④
【答案】B
【解析】
根据三角形的中位线定理“三角形的中位线平行于第三边”同时利用全等三角形的性质求解.
如下图所示:连接AC,延长BD交AC于点M,延长AD交BC于Q,延长CD交AB于P.∵∠ABC=∠C=45°,∴CP⊥AB,∵∠ABC=∠A=45°,∴AQ⊥BC,点D为两条高的交点,所以BM为AC边上的高,即:BM⊥AC,由中位线定理可得EF∥AC,EF=![]() AC,∴BD⊥EF,故①正确;∵∠DBQ+∠DCA=45°,∠DCA+∠CAQ=45°,∴∠DBQ=∠CAQ,∵∠A=∠ABC,∴AQ=BQ,∵∠BQD=∠AQC=90°,∴根据以上条件得△AQC≌△BQD,∴BD=AC,∴EF=
AC,∴BD⊥EF,故①正确;∵∠DBQ+∠DCA=45°,∠DCA+∠CAQ=45°,∴∠DBQ=∠CAQ,∵∠A=∠ABC,∴AQ=BQ,∵∠BQD=∠AQC=90°,∴根据以上条件得△AQC≌△BQD,∴BD=AC,∴EF=![]() AC,故②正确;∵∠A=∠ABC=∠C=45°,∴∠DAC+∠DCA=180°(∠A+∠ABC+∠C)=45°,∴∠ADC=180°(∠DAC+∠DCA)=135°=∠BEF+∠BFE=180°∠ABC,故③∠ADC=∠BEF+∠BFE成立;无法证明AD=CD,故④错误.故选B.
AC,故②正确;∵∠A=∠ABC=∠C=45°,∴∠DAC+∠DCA=180°(∠A+∠ABC+∠C)=45°,∴∠ADC=180°(∠DAC+∠DCA)=135°=∠BEF+∠BFE=180°∠ABC,故③∠ADC=∠BEF+∠BFE成立;无法证明AD=CD,故④错误.故选B.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋里装有2个相同的小球,它们分别写有数字1和2;乙口袋里装有3个相同的小球,它们分别写有数字3,4,5;丙口袋里有2个相同的小球,它们分别写有数字6,7,从三个口袋中各随机地取出1个小球,按要求解答下列问题:
(1)画出“树形图”;
(2)取出的3个小球上只有1个偶数数字的概率是多少?
(3)取出的3个小球上全是奇数数字的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ADE经顺时针旋转后与△ABF重合.
(1)旋转中心是点________,旋转了________度.
(2)如果连接EF,那么△AEF是怎样的三角形?为什么?
(3)请用尺规作图画出△AEF的外接圆,标明圆心M的位置,量出半径的长度为________,并判断点C与⊙M的位置关系为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)(x+8)2=36;
(2)x(5x+4)-(4+5x)=0;
(3)x2+3=3(x+1);
(4)2x2-x-1=0(用配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
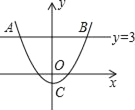
【题目】如图,抛物线y=ax2+c与直线y=3相交于点A,B,与y轴相交于点C(0,﹣1),其中点A的横坐标为﹣4.
(1)计算a,c的值;
(2)求出抛物线y=ax2+c与x轴的交点坐标;
(3)利用图象,当0≤ax2+c≤3时,直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).
(1)若点A在优弧![]() 上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= °.
上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= °.
(2)若四边形OBCD为平行四边形.
①当圆心O在∠BAD的内部时,求∠OBA+∠ODA的度数;
②当圆心O在∠BAD的外部时,请画出图形并直接写出∠OBA与∠ODA的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
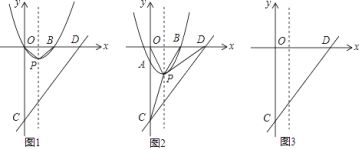
【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(1)写出点B坐标;判断△OBP的形状;
(2)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD= ![]() S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;
(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D,E,F分别是△ABC各边的中点,下列说法中错误的是( )
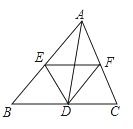
A. △ABC与△DEF是相似形 B. △ABC与△AEF是位似图形 C. EF与AD互相平分 D. AD平分∠BAC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com