
����Ŀ����ͼ���ı���OBCD�е����������ڡ�O�ϣ���A�ǡ�O�ϵ�һ�����㣨�����B��C��D�غϣ���
��1������A���Ż�![]() �ϣ���Բ��O�ڡ�BAD���ڲ�����֪��BOD=120�������OBA+��ODA= �㣮
�ϣ���Բ��O�ڡ�BAD���ڲ�����֪��BOD=120�������OBA+��ODA= �㣮
��2�����ı���OBCDΪƽ���ı��Σ�
�ٵ�Բ��O�ڡ�BAD���ڲ�ʱ�����OBA+��ODA�Ķ�����
�ڵ�Բ��O�ڡ�BAD���ⲿʱ���뻭��ͼ�β�ֱ��д����OBA���ODA��������ϵ��

���𰸡���1��60������2����60�����ڡ�OBA=��ODA+60����
��������
���⣨1������BD������Բ�ܽǶ����������BAD�Ķ����Ƕ��٣�Ȼ����������ε��ڽǺͶ����������0BD����ODB�Ķ������Ƕ��٣��������ABD�У���180����ȥ��BAD����0BD����ODB�Ķ����ͣ������OBA+��ODA���ڶ��ټ��ɣ�
��2�������ȸ����ı���OBCDΪƽ���ı��Σ��ɵ���BOD=��BCD����OBC=��ODC��Ȼ�������BAD+��BCD=180������BAD=![]() ��B0D�������B0D�Ķ��������������BAD�Ķ�����������ƽ���ı��ε����ʣ������OBC����ODC�Ķ������ٸ�����ABC+��ADC=180���������OBA+��ODA���ڶ��ټ��ɣ�
��B0D�������B0D�Ķ��������������BAD�Ķ�����������ƽ���ı��ε����ʣ������OBC����ODC�Ķ������ٸ�����ABC+��ADC=180���������OBA+��ODA���ڶ��ټ��ɣ�
�����ȸ����ı���OBCDΪƽ���ı��Σ��ɵ���BOD=��BCD����OBC=��ODC��Ȼ�������BAD+��BCD=180������BAD=![]() ��B0D�������B0D�Ķ��������������BAD�Ķ�����������OA=OD��OA=OB���жϳ���OAD=��ODA����OAB=��OBA�������жϳ���OBA=��ODA+60�����ɣ�
��B0D�������B0D�Ķ��������������BAD�Ķ�����������OA=OD��OA=OB���жϳ���OAD=��ODA����OAB=��OBA�������жϳ���OBA=��ODA+60�����ɣ�
����������⣺��1����ͼ1������BD��
�ߡ�BOD=120����
���BAD=120���2=60����
���0BD+��ODB=180�㩁��BOD=180�㩁120��=60����
���OBA+��ODA=180�㩁����0BD+��ODB������BAD=180�㩁60�㩁60��=120�㩁60��=60����
�ʴ�Ϊ��60��
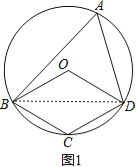
��2������ͼ2��
���ı���OBCDΪƽ���ı��Σ�
���BOD=��BCD����OBC=��ODC��
���ߡ�BAD+��BCD=180������BAD=![]() ��B0D��
��B0D��
��![]() ��B0D+��B0D=180����
��B0D+��B0D=180����
���B0D=120������BAD=120���2=60����
���OBC=��ODC=180�㩁120��=60����
���ߡ�ABC+��ADC=180����
���OBA+��ODA=180�㩁����OBC+��ODC��=180�㩁��60��+60����=180�㩁120��=60����
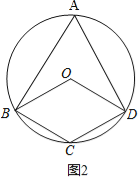
����ͼ3��
���ı���OBCDΪƽ���ı��Σ�
���BOD=��BCD����OBC=��ODC��
���ߡ�BAD+��BCD=180������BAD=![]() ��B0D��
��B0D��
��![]() ��B0D+��B0D=180����
��B0D+��B0D=180����
���B0D=120������BAD=120���2=60����
���OAB=��OAD+��BAD=��OAD+60����
��OA=OD��OA=OB��
���OAD=��ODA����OAB=��OBA��
���OBA=��ODA+60����
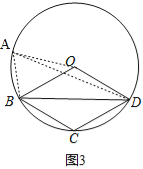


 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У�
��![]() ����
����![]() �DZ�
�DZ�![]() �ϵĶ��㣨���˵�
�ϵĶ��㣨���˵�![]() ��
��![]() ��������
��������![]() ����
����![]() ����ֱ��Ϊ�Գ�������
����ֱ��Ϊ�Գ�������![]() �ĶԳƵ�
�ĶԳƵ�![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() ��
��![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() ��
��

��1����֤���ı���![]() �����Σ�
������
��2�����ı���![]() �����Ϊ
�����Ϊ![]() ����
����![]() �ij���
�ij���
��3����![]() ��������Ϊ�ڱ߹���ƽ���ı��Σ����������ƽ���ı���ǡ��������ʱ����ʱ�����ε������________��
��������Ϊ�ڱ߹���ƽ���ı��Σ����������ƽ���ı���ǡ��������ʱ����ʱ�����ε������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
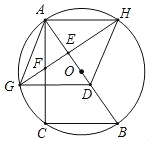
����Ŀ����ͼ��Rt��ABC��CA��BC��AC��4����AB����ȡһ��D��ʹAD��BC����AD�Ĵ�ֱƽ���ߣ���AC���ڵ�F������ABΪֱ���ġ�O��G��H����BC��x��
��1����֤���ı���AGDHΪ���Σ�
��2����EF��y����y����x�ĺ�����ϵʽ��
��3������OF��CG��
������AOF�������������O�������
����BC��3����![]() CG+9��______����ֱ��д���𰸣���
CG+9��______����ֱ��д���𰸣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A����ABC����C��45�㣬E��F�ֱ���AB��BC���е㣬�����н��ۣ���EF��BD����EF��![]() BD���ۡ�ADC����BEF+��BFE����AD��DC��������ȷ���ǣ�������
BD���ۡ�ADC����BEF+��BFE����AD��DC��������ȷ���ǣ�������
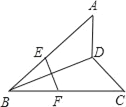
A. �٢ڢۢ� B. �٢ڢ� C. �٢ڢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�ֱ��y��kx+2�������ύ��A��B���㣬OA��4����C��x���������ϵĵ㣬��OC��OB������C��AB�Ĵ��ߣ���y���ڵ�D��������y��ax2+bx+c��A��B��C���㣮
��1���������ߺ�����ϵʽ��
��2����ͼ�ڣ���P������BA��һ���㣨�����B�غϣ�������OP������O��OP�Ĵ��߽�ֱ��CD�ڵ�Q����֤��OP��OQ��
��3����ͼ�ۣ��ڣ�2���������£��ֱ��P��Q������x��Ĵ��ߣ��ֱ�x���ڵ�E��F�����������ڵ�M��N���Ƿ���ڵ�P��λ�ã�ʹ��P��Q��M��NΪ������ı���Ϊƽ���ı��Σ�������ڣ������P�����ꣻ��������ڣ���˵�����ɣ�
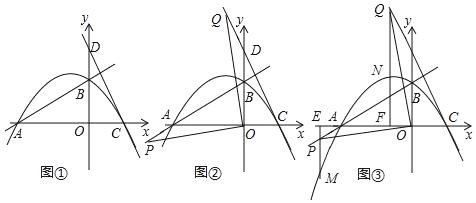
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У���P��BC����һ���㣨�����B��C�غϣ�������AP��������PD��ʹ��APD=60�㣬PD��AC�ڵ�D����֪AB=a����CD=y��BP=x����y��x������ϵ�Ĵ���ͼ���ǣ�������

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ԭ���������![]() ��
��![]() �����һ������Ϊ
�����һ������Ϊ![]() ���ֽ�����������ƽ��
���ֽ�����������ƽ��![]() ����λ���ȣ�������������
����λ���ȣ�������������![]() �ύ��
�ύ��![]() ����ԭ�����߽��ڵ�
����ԭ�����߽��ڵ�![]() ����
����![]() �����Ϊ
�����Ϊ![]() ������
������![]() ��ʾ
��ʾ![]() =__________
=__________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��1��3�������߶�OP��ԭ��O��˳ʱ�뷽����ת90���õ��߶�OP�������P���������ǣ� ��
A. ����1��3�� B. ��1����3�� C. ��3����1�� D. ��3��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB����O��ֱ���������DAB��ƽ����AC����O�ڵ�C����CD��AD������ΪD��ֱ��CD��AB���ӳ��߽��ڵ�E��
��1����֤��ֱ��CDΪ��O�����ߣ�
��2����AB��2BE����CE��ʱ����AD�ij���
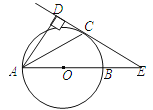
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com