
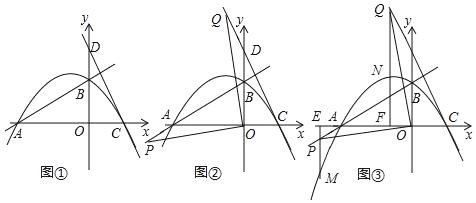
【题目】如图①,直线y=kx+2与坐标轴交于A、B两点,OA=4,点C是x轴正半轴上的点,且OC=OB,过点C作AB的垂线,交y轴于点D,抛物线y=ax2+bx+c过A、B、C三点.
(1)求抛物线函数关系式;
(2)如图②,点P是射线BA上一动点(不与点B重合),连接OP,过点O作OP的垂线交直线CD于点Q.求证:OP=OQ;
(3)如图③,在(2)的条件下,分别过P、Q两点作x轴的垂线,分别交x轴于点E、F,交抛物线于点M、N,是否存在点P的位置,使以P、Q、M、N为顶点的四边形为平行四边形?如果存在,求出点P的坐标;如果不存在,请说明理由.
【答案】(1) y=﹣![]() x2﹣
x2﹣![]() x+2; (2)见解析;(3)见解析.
x+2; (2)见解析;(3)见解析.
【解析】
(1)根据自变量与函数值的对应关系可得A、B点坐标,再根据OB=OC可得C点坐标,进而根据待定系数法可得抛物线解析式;(2)根据题意易得∠BAO=∠ODC,然后根据“ASA”证得△AOB≌△COD,进而可得OA=OD,∠OAD=∠ODQ,再根据∠POQ=∠AOD=90°得到∠AOP=∠DOQ,因此可证△AOP≌△DOQ,即可证OP=OQ;(3)设点P横坐标为n,则点P坐标为(n,![]() n+2),点M的坐标为(n,
n+2),点M的坐标为(n,![]() n2﹣
n2﹣![]() n+2),通过证△OPE≌△OQF(AAS)确定Q,N的坐标,由题意可得PM∥QN,故当PM=QN时,以P、Q、M、N为顶点的四边形为平行四边形,分P在M点上方以及P在M点下方两种情况进行讨论,根据PM=QN求出点P坐标即可.
n+2),通过证△OPE≌△OQF(AAS)确定Q,N的坐标,由题意可得PM∥QN,故当PM=QN时,以P、Q、M、N为顶点的四边形为平行四边形,分P在M点上方以及P在M点下方两种情况进行讨论,根据PM=QN求出点P坐标即可.
解:(1)∵OA=4
∴点A(﹣4,0)
∵直线y=kx+2与坐标轴交于A、B两点,
∴点B(0,2),0=﹣4k+2
∴OB=2,k=![]()
∴直线解析式y=![]() x+2
x+2
∵OC=OB=2
∴点C(2,0)
∵抛物线y=ax2+bx+c过A、B、C三点.
∴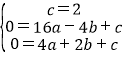 ,
,
解得:a=﹣![]() ,b=﹣
,b=﹣![]() ,c=2
,c=2
∴抛物线解析式:y=﹣![]() x2﹣
x2﹣![]() x+2;
x+2;
(2)∵CD⊥AB
∴∠BAO+∠DCO=90°
又∵∠ODC+∠DCO=90°
∴∠BAO=∠ODC且OB=OC,∠AOB=∠COD=90°
∴△AOB≌△COD(ASA)
∴OA=OD,∠OAB=∠ODC
∴∠OAP=∠ODQ
∵∠POQ=90°,∠AOD=90°
∴∠AOP=∠DOQ且OA=OD,∠OAP=∠ODQ
∴△AOP≌△DOQ(ASA)
∴OP=OQ
(3)设点P横坐标为n,则点P坐标为(n,![]() n+2),点M的坐标为(n,
n+2),点M的坐标为(n,![]() n2﹣
n2﹣![]() n+2)
n+2)
∵QF⊥x轴,
∴∠FQO+∠QOF=90°,且∠QOF+∠POE=90°
∴∠FQO=∠EOP
又∵∠OEP=∠QFO=90°,OP=OQ
∴△OPE≌△OQF(AAS)
∴OE=QF,PE=OF
∴点Q的坐标为(![]() n+2,﹣n),点N坐标(
n+2,﹣n),点N坐标(![]() n+2,﹣
n+2,﹣![]() n2﹣
n2﹣![]() n).
n).
由题意可得PM∥QN
当PM=QN时,以P、Q、M、N为顶点的四边形为平行四边形
当点P位于点M上方时:如图:
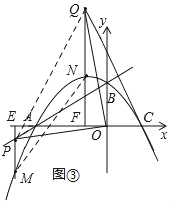
∴PM=(![]() n+2)﹣(
n+2)﹣(![]() n2﹣
n2﹣![]() n+2)=
n+2)=![]() n2+n
n2+n
QN=(﹣n)﹣(﹣![]() n2﹣
n2﹣![]() n)=
n)=![]() n2﹣
n2﹣![]() n
n
∴![]() n2﹣
n2﹣![]() n=
n=![]() n2+n
n2+n
解得:n=0(不合题意舍去),n=﹣![]()
∴![]() ×(﹣
×(﹣![]() )+2=﹣
)+2=﹣![]()
∴点P坐标为(﹣![]() ,﹣
,﹣![]() )
)
当点P位于点M下方时,如图:

∴PM=(![]() n2﹣
n2﹣![]() n+2)﹣(
n+2)﹣(![]() n+2)=﹣
n+2)=﹣![]() n2﹣n
n2﹣n
QN=(﹣n)﹣(﹣![]() n2﹣
n2﹣![]() n)=
n)=![]() n2﹣
n2﹣![]() n
n
∴﹣![]() n2﹣n=
n2﹣n=![]() n2﹣
n2﹣![]() n
n
解得:n=0(不合题意舍去),n=﹣![]() ,
,
∴![]() ×(﹣
×(﹣![]() )+2=
)+2=![]()
∴点P的坐标为(﹣![]() ,
,![]() )
)
综上所述:点P坐标(﹣![]() ,﹣
,﹣![]() ),(﹣
),(﹣![]() ,
,![]() )
)


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】研究问题:一个不透明的盒中装有若干个白球,怎样估算白球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验.摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
统计结果如表:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到有记号球的次数m | 25 | 44 | 57 | 105 | 160 | 199 |
摸到有记号球的频率 | 0.25 | 0.22 | 0.19 | 0.21 | 0.20 | 0.20 |
(1)请你完成上表中数据,并估计摸到有记号球的概率是多少?
(2)估计盒中共有球多少个?没有记号球有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)(x+8)2=36;
(2)x(5x+4)-(4+5x)=0;
(3)x2+3=3(x+1);
(4)2x2-x-1=0(用配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外其余均相同的红、蓝两种球,已知其中红球有3个,且从中任意摸出一个是红球的概率为0.75.
(1)根据题意,袋中有 个蓝球.
(2)若第一次随机摸出一球,不放回,再随机摸出第二个球.请用画树状图或列表法求“摸到两球中至少一个球为蓝球(记为事件A)”的概率P(A).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).
(1)若点A在优弧![]() 上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= °.
上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= °.
(2)若四边形OBCD为平行四边形.
①当圆心O在∠BAD的内部时,求∠OBA+∠ODA的度数;
②当圆心O在∠BAD的外部时,请画出图形并直接写出∠OBA与∠ODA的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某政府在广场上树立了如图所示的宣传牌,数学兴趣小组的同学想利用所学的知识测量宣传牌的高度AB,在D处测得点A、B的仰角分别为38°、21°,已知CD=20m,点A、B、C在一条直线上,AC⊥DC,求宣传牌的高度AB(sin21°≈0.36,cos21°≈0.93,tan21°≈0.38,sin38°≈0.62,cos38°≈0.78,tan38°≈0.79,结果精确到1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 是坐标原点,四边形
是坐标原点,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的负半轴上,直线
轴的负半轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() .
.
(1)如图1,求直线![]() 的解析式;
的解析式;

(2)如图2,连接![]() ,动点
,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 方向以1个单位/秒的速度向终点
方向以1个单位/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() (
(![]() ),点
),点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长是:
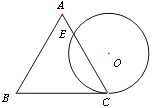
A. ![]() B.
B. ![]() C. 2 D. 3
C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com