
【题目】研究问题:一个不透明的盒中装有若干个白球,怎样估算白球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验.摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
统计结果如表:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到有记号球的次数m | 25 | 44 | 57 | 105 | 160 | 199 |
摸到有记号球的频率 | 0.25 | 0.22 | 0.19 | 0.21 | 0.20 | 0.20 |
(1)请你完成上表中数据,并估计摸到有记号球的概率是多少?
(2)估计盒中共有球多少个?没有记号球有多少个?
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如果一元二次方程ax2+bx+c=0 的两根 x1,x2均为正数,其中x1>x2,且满足1<x1﹣x2<2,那么称这个方程有“友好根”.
(1)方程(x﹣![]() )(x﹣
)(x﹣![]() )=0_____“友好根”(填:“有”或“没有”);
)=0_____“友好根”(填:“有”或“没有”);
(2)已知关于x的 x2﹣(t﹣1)x+t﹣2=0有“友好根”,求 t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=﹣![]() ,下列结论:①图象必经过点(﹣3,1);②图象在第二,四象限内;③y随x的增大而增大;④当x>﹣1时,y>3.其中错误的结论有( )
,下列结论:①图象必经过点(﹣3,1);②图象在第二,四象限内;③y随x的增大而增大;④当x>﹣1时,y>3.其中错误的结论有( )
A. ①④ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
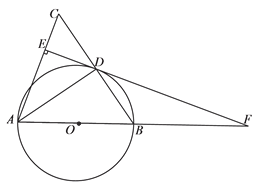
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线.
(2)如果⊙O的半径为5,sin∠ADE=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
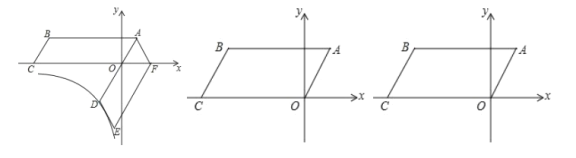
【题目】如图,在平面直角坐标系中,四边形![]() 为平行四边形,
为平行四边形,![]() 为坐标原点,
为坐标原点,![]() ,将平行四边形
,将平行四边形![]() 绕点
绕点![]() 逆时针旋转得到平行四边形
逆时针旋转得到平行四边形![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 落在
落在![]() 轴正半轴上.
轴正半轴上.
(1)证明:![]() 是等边三角形:
是等边三角形:
(2)平行四边形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 度
度![]() .
.![]() 的对应线段为
的对应线段为![]() ,点
,点![]() 的对应点为
的对应点为![]()
①直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标:
的坐标:
②对角线![]() 在旋转过程中设点
在旋转过程中设点![]() 坐标为
坐标为![]() ,当点
,当点![]() 到
到![]() 轴的距离大于或等于
轴的距离大于或等于![]() 时,求
时,求![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上的动点(含端点
上的动点(含端点![]() ,
,![]() ),连结
),连结![]() ,以
,以![]() 所在直线为对称轴作点
所在直线为对称轴作点![]() 的对称点
的对称点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() ,
,![]() 的中点,连结
的中点,连结![]() ,
,![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的长;
的长;
(3)以![]() 其中两边为邻边构造平行四边形,当所构造的平行四边形恰好是菱形时,这时该菱形的面积是________.
其中两边为邻边构造平行四边形,当所构造的平行四边形恰好是菱形时,这时该菱形的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,点
,点![]() .已知抛物线
.已知抛物线![]() (
(![]() 是常数),顶点为
是常数),顶点为![]() .
.
(Ⅰ)当抛物线经过点![]() 时,求顶点
时,求顶点![]() 的坐标;
的坐标;
(Ⅱ)若点![]() 在
在![]() 轴下方,当
轴下方,当![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(Ⅲ) 无论![]() 取何值,该抛物线都经过定点
取何值,该抛物线都经过定点![]() .当
.当![]() 时,求抛物线的解析式.
时,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
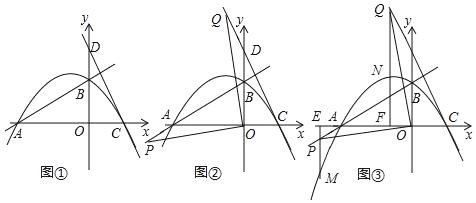
【题目】如图①,直线y=kx+2与坐标轴交于A、B两点,OA=4,点C是x轴正半轴上的点,且OC=OB,过点C作AB的垂线,交y轴于点D,抛物线y=ax2+bx+c过A、B、C三点.
(1)求抛物线函数关系式;
(2)如图②,点P是射线BA上一动点(不与点B重合),连接OP,过点O作OP的垂线交直线CD于点Q.求证:OP=OQ;
(3)如图③,在(2)的条件下,分别过P、Q两点作x轴的垂线,分别交x轴于点E、F,交抛物线于点M、N,是否存在点P的位置,使以P、Q、M、N为顶点的四边形为平行四边形?如果存在,求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com