
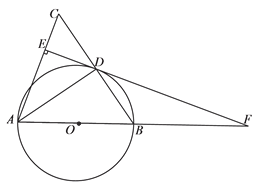
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线.
(2)如果⊙O的半径为5,sin∠ADE=![]() ,求BF的长.
,求BF的长.
【答案】(1)答案见解析;(2)![]() .
.
【解析】试题分析:(1)连接OD,AB为⊙O的直径得∠ADB=90°,由AB=AC,根据等腰三角形性质得AD平分BC,即DB=DC,则OD为△ABC的中位线,所以OD∥AC,而DE⊥AC,则OD⊥DE,然后根据切线的判定方法即可得到结论;
(2)由∠DAC=∠DAB,根据等角的余角相等得∠ADE=∠ABD,在Rt△ADB中,利用解直角三角形的方法可计算出AD=8,在Rt△ADE中可计算出AE=![]() ,然后由OD∥AE,得△FDO∽△FEA,再利用相似比可计算出BF.
,然后由OD∥AE,得△FDO∽△FEA,再利用相似比可计算出BF.
试题解析:(1)证明:连结OD
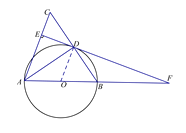
∵OD=OB∴∠ODB=∠DBO
又AB=AC
∴∠DBO=∠C
∴∠ODB =∠C
∴OD ∥AC
又DE⊥AC
∴DE ⊥OD
∴EF是⊙O的切线.
(2)∵AB是直径
∴∠ADB=90 °
∴∠ADC=90 °
即∠1+∠2=90 °又∠C+∠2=90 °
∴∠1=∠C
∴∠1 =∠3
∴![]()
∴![]()
∴AD=8
在Rt△ADB中,AB=10∴BD=6
在又Rt△AED中, ![]()
∴![]()
设BF=x
∵OD ∥AE
∴△ODF∽△AEF
∴![]() ,即
,即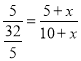 ,
,
解得:x=![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
∵![]()
∴![]()
解答问题:
(1)在式![]() 中,第六项为 ,第n项为 ,上述求和的想法是通过逆用 法则,将式中各分数转化为两个实数之差,使得除首末两项外的中间各项可以 从而达到求和的目的.
中,第六项为 ,第n项为 ,上述求和的想法是通过逆用 法则,将式中各分数转化为两个实数之差,使得除首末两项外的中间各项可以 从而达到求和的目的.
(2)解方程![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,正方形OBAC的顶点A的坐标为(8,8),点D,E分别为边AB,AC上的动点,且不与端点重合,连接OD,OE,分别交对角线BC于点M,N,连接DE,若∠DOE=45°, 以下说法正确的是________(填序号).
①点O到线段DE的距离为8;②△ADE的周长为16;③当DE∥BC时,直线OE的解析式为y=![]() x; ④以三条线段BM,MN,NC为边组成的三角形是直角三角形.
x; ④以三条线段BM,MN,NC为边组成的三角形是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(5分)(2015春鞍山期末)小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 5 | 50 |
(1)请将表格补充完整;
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在平行四边形,矩形,菱形、正方形中,一定是十字形的有 ;
②若凸四边形ABCD是十字形,AC=a,BD=b,则该四边形的面积为 ;
(2)如图1,以等腰Rt△ABC的底边AC为边作等边三角形△ACD,连接BD,交AC于点O, 当 ![]() ≤S 四边形≤
≤S 四边形≤![]() 时,求BD的取值范围;
时,求BD的取值范围;
(3)如图2,以十字形ABCD的对角线AC与BD为坐标轴,建立如图所示的平面直角坐标系xOy,若计 十字形ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为:S1,S2,S3,S4,且同时满足列四个条件:

①![]() ;②
;② ![]() ;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,函数![]() (x<0)的图象与直线y=x+2交于点A(-3,m).
(x<0)的图象与直线y=x+2交于点A(-3,m).
(1)求k,m的值;
(2)已知点P(a,b)是直线y=x上,位于第三象限的点,过点P作平行于x轴的直线,交直线y=x+2于点M,过点P作平行于y轴的直线,交函数![]() (x<0)的图象于点N.
(x<0)的图象于点N.
①当a=-1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM结合函数的图象,直接写出b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为美化学校环境,建设绿色校园,陶治师生情操我校计划用180元购买A、B两种花卉苗共20棵,已知A种花卉苗每棵12元,B种花卉苗每棵8元.
(1)根据题意,甲、乙两个同学分别列出了尚不完整的方程组如下:
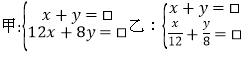
根据甲、乙两名同学所列的方程组,请你分别指出未知数x,y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示 ,y表示 ;
乙:x表示 ,y表示 ;
(2)求A、B两种花卉各多少棵?(写出完整的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店出售一种水果,每只定价20元时,每周可卖出300只.试销发现:
①每只水果每降价1元,每周可多卖出25只;
②每只水果每涨价1元,每周将少卖出10只;
③水果定价不能低于18元.
我们知道,销售收入=销售单价×销售量,设降价出售时的销售收入为y1元,涨价出售时的销售收入为y2元,水果的定价为x元/只.
根据以上信息,回答下列问题:
(1)请直接写出y1、y2与x的函数关系式,并写出x的取值范围;
y1= ;y2= ;
(2)你认为应当如何定价才能使一周的销售收入最多?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com