
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在平行四边形,矩形,菱形、正方形中,一定是十字形的有 ;
②若凸四边形ABCD是十字形,AC=a,BD=b,则该四边形的面积为 ;
(2)如图1,以等腰Rt△ABC的底边AC为边作等边三角形△ACD,连接BD,交AC于点O, 当 ![]() ≤S 四边形≤
≤S 四边形≤![]() 时,求BD的取值范围;
时,求BD的取值范围;
(3)如图2,以十字形ABCD的对角线AC与BD为坐标轴,建立如图所示的平面直角坐标系xOy,若计 十字形ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为:S1,S2,S3,S4,且同时满足列四个条件:

①![]() ;②
;② ![]() ;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
【答案】(1)①菱形和正方形;②![]() ab;(2)
ab;(2)![]() ≤BD≤2;(3)点P走完全程所需的时间t=
≤BD≤2;(3)点P走完全程所需的时间t=![]() ,直线EF的解析式为y=
,直线EF的解析式为y=![]() x+
x+![]() .
.
【解析】
(1)①根据菱形,正方形和矩形的性质即可判断;
②根据对角线互相垂直的四边形的面积等于对角线乘积的一半计算即可;
(2)设AC的长为x,根据△ABC为等腰直角三角形,△ACD为等边三角形,得出OB=![]() x,OD=
x,OD=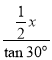 =
=![]() x,即BD=
x,即BD=![]() x+
x+![]() x,再根据
x,再根据![]() ≤S四边形≤
≤S四边形≤![]() 运算即可;
运算即可;
(3)首先设A(-a,0),B(0,b),C(c,0),D(0,-d),然后根据![]() ,
,![]() ,得出a=c,b=d,再结合已知条件推吹四边形ABCD是有一个角为60°的菱形,根据菱形ABCD的周长为32,即可得出AB=8,OA=4,OB=
,得出a=c,b=d,再结合已知条件推吹四边形ABCD是有一个角为60°的菱形,根据菱形ABCD的周长为32,即可得出AB=8,OA=4,OB=![]() ,OE=2,过F点作FM⊥BC交BC于M点,可得FM=FBsin30°=
,OE=2,过F点作FM⊥BC交BC于M点,可得FM=FBsin30°=![]() FB,可得点P的运动时间t=
FB,可得点P的运动时间t=![]() =EF+
=EF+![]() FB=EF+FM,当E,F,M三点共线时EF+FM的值最小,由此可推出t=
FB=EF+FM,当E,F,M三点共线时EF+FM的值最小,由此可推出t=![]() ;根据在Rt△EOF中,OE=2,∠FEO=30°,可推出F(0,
;根据在Rt△EOF中,OE=2,∠FEO=30°,可推出F(0,![]() ),再结合点E的坐标为(-2,0),即可求出EF的解析式.
),再结合点E的坐标为(-2,0),即可求出EF的解析式.
(1)①∵菱形和正方形的对角线互相垂直,矩形的对角线不互相垂直,
∴菱形和正方形一定是十字形;
②对角线互相垂直的四边形的面积等于对角线乘积的一半,
∴四边形的面积为![]() ab;
ab;
(2)设AC的长为x,
∵△ABC为等腰直角三角形,△ACD为等边三角形,
∴OB=![]() x,OD=
x,OD=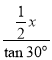 =
=![]() x,
x,
∴BD=![]() x+
x+![]() x,
x,
∵![]() ≤S四边形≤
≤S四边形≤![]()
![]() ≤
≤![]() x(
x(![]() x+
x+![]() x)≤
x)≤![]()
![]() ≤
≤![]() x2≤
x2≤![]()
![]() ≤x2≤
≤x2≤![]()
![]() ≤x≤
≤x≤![]()
∴![]() ≤
≤![]() x≤
x≤![]()
即![]() ≤BD≤2;
≤BD≤2;
(3)设A(-a,0),B(0,b),C(c,0),D(0,-d),
∴S1=![]() ab,S2=
ab,S2=![]() cd,S3=
cd,S3=![]() ad,S4=
ad,S4=![]() bc,
bc,
∵![]() ,
,![]() ,
,
∴S=S1+S2+![]() =
=![]() ab+
ab+![]() cd+
cd+![]() ,
,
S=S3+S4+![]() =
=![]() ad+
ad+![]() bc+
bc+![]() ,
,
即![]() ab+
ab+![]() cd=
cd=![]() ad+
ad+![]() bc
bc
![]() ab-
ab-![]() ad=
ad=![]() bc-
bc-![]() cd
cd
![]() a(b-d)=
a(b-d)=![]() c(b-d)
c(b-d)
即a=c,同理b=d,
∴△AOB≌△BOC,△AOB≌△AOD,
∴AB=BC,AB=AD,
∵∠ABC=60°,
∴四边形ABCD是有一个角为60°的菱形,
∵菱形ABCD的周长为32,
∴AB=8,OA=4,OB=![]() ,
,
∵点E为OA的中点,
∴OE=2,
过F点作FM⊥BC交BC于M点,可得FM=FBsin30°=![]() FB,
FB,
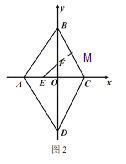
∴点P的运动时间t=![]() =EF+
=EF+![]() FB=EF+FM,
FB=EF+FM,
∴当E,F,M三点共线时EF+FM的值最小,
∵∠ECM=60°,AC=AB,点E为OA的中点,
∴CE=6,∠∠FEO=30°,E(-2,0),
∴CM=3,EM=![]() ,即t=
,即t=![]() ,
,
在Rt△EOF中,OE=2,∠FEO=30°,
∴OF=![]() ,即F(0,
,即F(0,![]() ),
),
∴设EF的解析式为y=kx+b,
将E,F的坐标代入得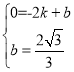 ,
,
解得: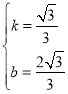 ,
,
∴EF的解析式为y=![]() x+
x+![]() ,
,
综上:点P走完全程所需的时间t=![]() ,直线EF的解析式为y=
,直线EF的解析式为y=![]() x+
x+![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
(1)当△CDQ≌△CPQ时,求AQ=_________;
(2)取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ=___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,
,![]() ,线段
,线段![]() 经过平移得到线段
经过平移得到线段![]() ,其中点
,其中点![]() 的对应点为点
的对应点为点![]() ,点D在第一象限,直线AC交
,点D在第一象限,直线AC交![]() 轴于点
轴于点![]()
(1)点D坐标为
(2)线段![]() 由线段
由线段![]() 经过怎样平移得到?
经过怎样平移得到?
(3)求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,□ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.
(1)求证:四边形 ABCD 是菱形;
(2)若∠ADC=60°,BE=2,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日是世界读书日,某校为了营造读书好、好读书、读好书的书香校园,决定采购《简·爱》、《小词大雅》两种图书供学生阅读,通过了解,购买2本《简·爱》和3本《小词大雅》共需168元,购买3本《简·爱》和2本《小词大雅》共需172元.
(1)求一本《简·爱》和《小词大雅》的价格分别是多少元;
(2)若该校计划购买两种图书共300本,其中《简·爱》的数量不多于《小词大雅》数量,且不少于100件.购买《简·爱》m本,求总费用W元与m之间的函数关系式,并写出m的取值范围;
(3)在(2)的条件下,学校在团购书籍时,商家店铺中《简·爱》正进行书籍促销活动,每本书箱降价a元(0< a <8),求学校购书的的最低总费用W1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
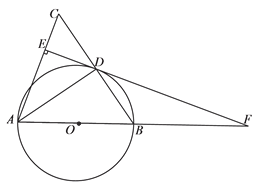
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线.
(2)如果⊙O的半径为5,sin∠ADE=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数![]() 的图象经过点A(1,4),B(m,n).
的图象经过点A(1,4),B(m,n).
(1)求反比例函数![]() 的解析式;
的解析式;
(2)若二次函数![]() 的图象经过点B,求代数式
的图象经过点B,求代数式![]() 的值;
的值;
(3)若反比例函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象只有一个交点,且该交点在直线y=x的下方,结合函数图象,求a的取值范围.
的图象只有一个交点,且该交点在直线y=x的下方,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
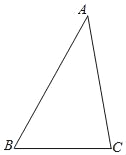
【题目】如图,在△ABC中,BC=3![]() ,AC=5,∠B=45°,则下面结论正确的是_____.
,AC=5,∠B=45°,则下面结论正确的是_____.
①∠C一定是钝角;
②△ABC的外接圆半径为3;
③sinA=![]() ;
;
④△ABC外接圆的外切正六边形的边长是![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B在反比例函数![]() (x>0)的图象上,它们的横坐标分别为m,n,且m≠n,过点A,点B都向x轴,y轴作垂线段,其中两条垂线段的交点为C.
(x>0)的图象上,它们的横坐标分别为m,n,且m≠n,过点A,点B都向x轴,y轴作垂线段,其中两条垂线段的交点为C.

(1)如图,当m=2,n=6时,直接写出点C的坐标:
(2)若A(m,n),B(n,m).连接OA、OB、AB,求△AOB的面积:(用含m的代数式表示)
(3)设AD⊥y轴于点D,BE⊥x轴于点E.若![]() ,且
,且![]() ,则当点C在直线DE上时,求p的取值范围.
,则当点C在直线DE上时,求p的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com