
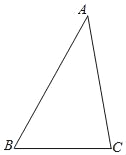
【题目】如图,在△ABC中,BC=3![]() ,AC=5,∠B=45°,则下面结论正确的是_____.
,AC=5,∠B=45°,则下面结论正确的是_____.
①∠C一定是钝角;
②△ABC的外接圆半径为3;
③sinA=![]() ;
;
④△ABC外接圆的外切正六边形的边长是![]() .
.
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点
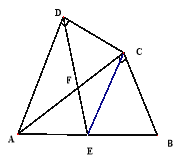
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在平行四边形,矩形,菱形、正方形中,一定是十字形的有 ;
②若凸四边形ABCD是十字形,AC=a,BD=b,则该四边形的面积为 ;
(2)如图1,以等腰Rt△ABC的底边AC为边作等边三角形△ACD,连接BD,交AC于点O, 当 ![]() ≤S 四边形≤
≤S 四边形≤![]() 时,求BD的取值范围;
时,求BD的取值范围;
(3)如图2,以十字形ABCD的对角线AC与BD为坐标轴,建立如图所示的平面直角坐标系xOy,若计 十字形ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为:S1,S2,S3,S4,且同时满足列四个条件:

①![]() ;②
;② ![]() ;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为美化学校环境,建设绿色校园,陶治师生情操我校计划用180元购买A、B两种花卉苗共20棵,已知A种花卉苗每棵12元,B种花卉苗每棵8元.
(1)根据题意,甲、乙两个同学分别列出了尚不完整的方程组如下:
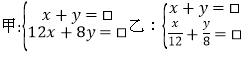
根据甲、乙两名同学所列的方程组,请你分别指出未知数x,y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示 ,y表示 ;
乙:x表示 ,y表示 ;
(2)求A、B两种花卉各多少棵?(写出完整的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
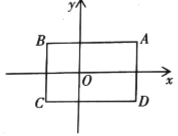
【题目】如图,在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,
,![]() ,把一根长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在
,把一根长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在![]() 处,并按
处,并按![]() 的规律紧绕在四边形
的规律紧绕在四边形![]() 的边上,则细线的另一端点所在位置的坐标是__________.
的边上,则细线的另一端点所在位置的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
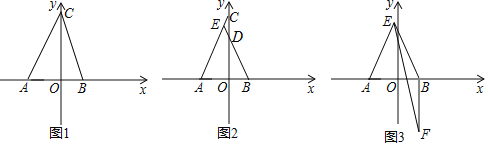
【题目】如图点A(a,0)在x轴负半轴,点B(b,0)在x轴正半轴,点C(0,c)在y轴正半轴,且![]() .
.
(1)如图1,求S△ABC;
(2)如图2,若点D(0,5),BD的延长线交AC于E,求∠AEB;
(3)如图3,在(2)的条件下,将线段BA绕点B逆时针旋转90°至线段BF,连接EF,试探究EA,EB,EF之间有怎样的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com