
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点
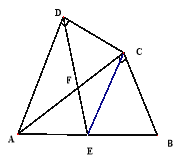
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求![]() 的值.
的值.
【答案】(1)见解析证明;(2)见解析证明;(3)![]() .
.
【解析】
试题分析:(1)由AC平分∠DAB,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=ABAD;(2)由E为AB的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE=![]() AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得
AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得![]() 的值.
的值.
试题解析:(1)∵AC平分∠DAB,∴∠DAC=∠CAB,∵∠ADC=∠ACB=90°,∴△ADC∽△ACB,∴AD:AC=AC:AB,∴![]() =ABAD;
=ABAD;
(2)∵E为AB的中点,∴CE=![]() AB=AE,∴∠EAC=∠ECA,∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥AD;
AB=AE,∴∠EAC=∠ECA,∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥AD;
(3)∵CE∥AD,∴△AFD∽△CFE,∴AD:CE=AF:CF,∵CE=![]() AB,∴CE=
AB,∴CE=![]() ×6=3,∵AD=4,∴
×6=3,∵AD=4,∴![]() =
=![]() ,∴
,∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
(1)当△CDQ≌△CPQ时,求AQ=_________;
(2)取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ=___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.

⑴写出A′、B′、C′的坐标;
⑵求出△ABC的面积;
⑶点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
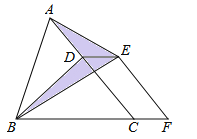
【题目】如图,已知△ABC的面积为24,点D在线段AC上,点D在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连结PO并延长交BC于点Q,设运动时间为t(0<t<5).
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.

 备用图
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,
,![]() ,线段
,线段![]() 经过平移得到线段
经过平移得到线段![]() ,其中点
,其中点![]() 的对应点为点
的对应点为点![]() ,点D在第一象限,直线AC交
,点D在第一象限,直线AC交![]() 轴于点
轴于点![]()
(1)点D坐标为
(2)线段![]() 由线段
由线段![]() 经过怎样平移得到?
经过怎样平移得到?
(3)求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,□ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.
(1)求证:四边形 ABCD 是菱形;
(2)若∠ADC=60°,BE=2,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
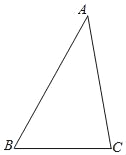
【题目】如图,在△ABC中,BC=3![]() ,AC=5,∠B=45°,则下面结论正确的是_____.
,AC=5,∠B=45°,则下面结论正确的是_____.
①∠C一定是钝角;
②△ABC的外接圆半径为3;
③sinA=![]() ;
;
④△ABC外接圆的外切正六边形的边长是![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com