
【题目】如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
(1)当△CDQ≌△CPQ时,求AQ=_________;
(2)取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ=___________.

【答案】![]() 2
2
【解析】
(1)由全等三角形的性质得到DQ=PQ,PC=DC=5,然后利用勾股定理求解即可.
(2)过M作EF⊥CD于F,则EF⊥AB,先证得△MDF≌△PME,得出ME=DF=![]() ,然后用梯形的中位线的性质定理求解即可.
,然后用梯形的中位线的性质定理求解即可.
(1)∵△CDQ≌△CPQ,
∴DQ=PQ,PC=DC,
∵AB=DC=5,AD=BC=3,
∴PC=5,
在RT△PBC中,![]() ,
,
∴PA=AB﹣PB=5﹣4=1,
设AQ=x,则DQ=PQ=3﹣x,
在RT△PAQ中,![]() ,
,
解得![]() ,∴AQ=
,∴AQ=![]() .
.
(2))如图2,过M作EF⊥CD于F,则EF⊥AB,
∵MD⊥MP,∴∠PMD=90°,∴∠PME+∠DMF=90°,
∵∠FDM+∠DMF=90°,∴∠MDF=∠PME,
∵M是QC的中点,根据直角三角形直线的性质求得DM=PM=![]() QC,
QC,
在△MDF和△PME中,∵∠MDF=∠PME,∠DFM=∠MEP,DM=PM,
∴△MDF≌△PME(AAS),∴ME=DF,PE=MF,
∵EF⊥CD,AD⊥CD,
∴EF∥AD,
∵QM=MC,
∴DF=CF=![]() DC=
DC=![]() ,
,
∴ME=![]() ,
,
∵ME是梯形ABCQ的中位线,
∴2ME=AQ+BC,即5=AQ+3,
∴AQ=2.



科目:初中数学 来源: 题型:
【题目】目前![]() 节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
室内用节能灯 | 40 | 58 |
室外用节能灯 | 50 | 70 |
(1)若该分店共购进节能灯1700盏,问购进的室内用、室外用节能灯各多少盏?
(2)若该分店将进货全部售完后获利要不少于32000元,问至少需要购进多少盏室内用节能灯?
(3)挂职锻炼的大学生村官王祥自酬了4650元在该分店购买这两种类型的节能灯若干盏,分发给村民使用,其中室内用节能灯盏数不少于室内用节能灯盏数的2倍,问王祥最多购买室外用节能灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某牧区需要550顶帐篷过冬,现由甲、乙两个工厂生产,已知甲工厂每天生产的能力是乙工厂的1.5倍,并且生产240顶帐篷甲工厂比乙工厂少4天,
(1)甲、乙两个工厂每天分别生产多少顶帐篷?
(2)若甲工厂每天生产成本为3万元,乙工厂每天生产成本为2.4万元,要使这批帐篷的生产总成本不高于60万元,至少应安排甲工厂生产多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
∵![]()
∴![]()
解答问题:
(1)在式![]() 中,第六项为 ,第n项为 ,上述求和的想法是通过逆用 法则,将式中各分数转化为两个实数之差,使得除首末两项外的中间各项可以 从而达到求和的目的.
中,第六项为 ,第n项为 ,上述求和的想法是通过逆用 法则,将式中各分数转化为两个实数之差,使得除首末两项外的中间各项可以 从而达到求和的目的.
(2)解方程![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
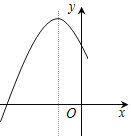
【题目】如图是二次函数![]() 图象的一部分,图象过点A(-3,0),对称轴为直线
图象的一部分,图象过点A(-3,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若B(
;④若B(![]() ,
, ![]() )、C(
)、C(![]() ,
, ![]() )为函数图象上的两点,则
)为函数图象上的两点,则![]() .其中正确结论是( )
.其中正确结论是( )
A. ②④ B. ①③ C. ①④ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点
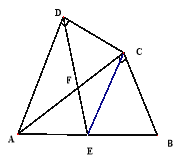
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在平行四边形,矩形,菱形、正方形中,一定是十字形的有 ;
②若凸四边形ABCD是十字形,AC=a,BD=b,则该四边形的面积为 ;
(2)如图1,以等腰Rt△ABC的底边AC为边作等边三角形△ACD,连接BD,交AC于点O, 当 ![]() ≤S 四边形≤
≤S 四边形≤![]() 时,求BD的取值范围;
时,求BD的取值范围;
(3)如图2,以十字形ABCD的对角线AC与BD为坐标轴,建立如图所示的平面直角坐标系xOy,若计 十字形ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为:S1,S2,S3,S4,且同时满足列四个条件:

①![]() ;②
;② ![]() ;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com