
【题目】某水果店出售一种水果,每只定价20元时,每周可卖出300只.试销发现:
①每只水果每降价1元,每周可多卖出25只;
②每只水果每涨价1元,每周将少卖出10只;
③水果定价不能低于18元.
我们知道,销售收入=销售单价×销售量,设降价出售时的销售收入为y1元,涨价出售时的销售收入为y2元,水果的定价为x元/只.
根据以上信息,回答下列问题:
(1)请直接写出y1、y2与x的函数关系式,并写出x的取值范围;
y1= ;y2= ;
(2)你认为应当如何定价才能使一周的销售收入最多?请说明理由.
科目:初中数学 来源: 题型:
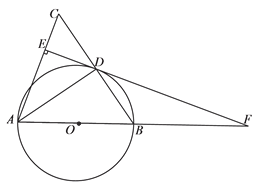
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线.
(2)如果⊙O的半径为5,sin∠ADE=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三人站成一横排照相,因甲、乙两人是好友,照相时两人紧邻着站在一起不分开.
(1)请按左、中、右的顺序列出所有符合要求的站位的结果;
(2)按要求随机的站立,求丙站在甲左边的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B在反比例函数![]() (x>0)的图象上,它们的横坐标分别为m,n,且m≠n,过点A,点B都向x轴,y轴作垂线段,其中两条垂线段的交点为C.
(x>0)的图象上,它们的横坐标分别为m,n,且m≠n,过点A,点B都向x轴,y轴作垂线段,其中两条垂线段的交点为C.

(1)如图,当m=2,n=6时,直接写出点C的坐标:
(2)若A(m,n),B(n,m).连接OA、OB、AB,求△AOB的面积:(用含m的代数式表示)
(3)设AD⊥y轴于点D,BE⊥x轴于点E.若![]() ,且
,且![]() ,则当点C在直线DE上时,求p的取值范围.
,则当点C在直线DE上时,求p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用棋子摆成的“Τ”字图案.从图案中可以看出,第1个“Τ”字型图案需要5枚棋子.第2个“Τ”字型图案需要8枚棋子.第3个“Τ”字型图案需要11枚棋子,则第n个“Τ”字型所需棋子的个数( )

A.2n+3 B.3n+2 C.3n+4 D.3n+5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC.
(1)求证:AC平分∠BAD;
(2)若AB=6,AC=4![]() ,求EC和PB的长.
,求EC和PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+(k-1)x-2k-3.
(1)求证:该二次函数图像与x轴总有两个公共点;
(2)若点A(-1,y1)、B(1,y2)在该二次函数的图像上,且y1>y2,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了8次测试,测试成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 10 | 8 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | 8 | 10 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙两名运动员8次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com