
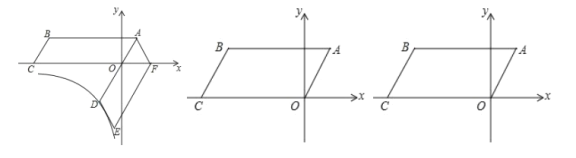
【题目】如图,在平面直角坐标系中,四边形![]() 为平行四边形,
为平行四边形,![]() 为坐标原点,
为坐标原点,![]() ,将平行四边形
,将平行四边形![]() 绕点
绕点![]() 逆时针旋转得到平行四边形
逆时针旋转得到平行四边形![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 落在
落在![]() 轴正半轴上.
轴正半轴上.
(1)证明:![]() 是等边三角形:
是等边三角形:
(2)平行四边形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 度
度![]() .
.![]() 的对应线段为
的对应线段为![]() ,点
,点![]() 的对应点为
的对应点为![]()
①直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标:
的坐标:
②对角线![]() 在旋转过程中设点
在旋转过程中设点![]() 坐标为
坐标为![]() ,当点
,当点![]() 到
到![]() 轴的距离大于或等于
轴的距离大于或等于![]() 时,求
时,求![]() 的范围.
的范围.
【答案】(1)见解析(2)①P(0, ![]() )或(0, -4)②-8≤m≤-
)或(0, -4)②-8≤m≤-![]() 或
或![]() ≤m≤12
≤m≤12
【解析】
(1)根据A点坐标求出∠AOF=60°,再根据旋转的特点得到AO=AF,故可求解;
(2)①设P(0,a)根据等腰三角形的性质分AP=OP和AO=OP,分别求出P点坐标即可;
②分旋转过程中![]() 在第三象限时
在第三象限时![]() 到
到![]() 轴的距离等于
轴的距离等于![]() 与旋转到第四象限时
与旋转到第四象限时![]() 到
到![]() 轴的距离等于
轴的距离等于![]() ,再求出当
,再求出当![]() 旋转180°时的坐标,即可得到m的取值.
旋转180°时的坐标,即可得到m的取值.
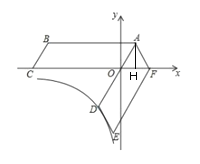
(1)如图,过A点作AH⊥x轴,
∵![]()
∴OH=2,AH=2![]()
∴AO=![]()
故AO=2OH
∴∠OAH=30°
∴∠AOF=90°-∠OAH=60°
∵旋转
∴AO=AF
∴△AOF是等边三角形;
(2)①设P(0,a)
∵![]() 是等腰三角形
是等腰三角形
当AP=OP时,(2-0)2+(2![]() -a)2=a2
-a)2=a2
解得a=![]()
∴P(0, ![]() )
)
当AO=OP时,OP= AO=4
∴P(0, -4)
故![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标是(0,
的坐标是(0, ![]() )或(0, -4);
)或(0, -4);
②旋转过程中点![]() 的对应点为
的对应点为![]() ,
,![]()
当![]() 开始旋转,至
开始旋转,至![]() 到
到![]() 轴的距离等于
轴的距离等于![]() 时,m的取值为-8≤m≤-
时,m的取值为-8≤m≤-![]() ;
;
当![]() 旋转到第四象限,到
旋转到第四象限,到![]() 轴的距离等于
轴的距离等于![]() 时,m=
时,m=![]()
当![]() 旋转180°时,设C’的坐标为(x,y)
旋转180°时,设C’的坐标为(x,y)
∵C、![]() 关于A点对称,
关于A点对称,
∴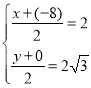
解得
∴![]() (12,
(12,![]() )
)
∴m的取值为![]() ≤m≤12,
≤m≤12,
综上,当点![]() 到
到![]() 轴的距离大于或等于
轴的距离大于或等于![]() 时,求
时,求![]() 的范围是-8≤m≤-
的范围是-8≤m≤-![]() 或
或![]() ≤m≤12.
≤m≤12.


科目:初中数学 来源: 题型:
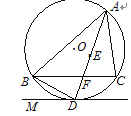
【题目】(本小题满分10分)
如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D;连接BD,过点D作直线DM,使∠BDM=∠DAC.
(1)求证:直线DM是⊙O的切线;
(2)求证:DE2=DF·DA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动.若以A、M、N为顶点的三角形与△ACD相似,则运动的时间t为________秒.
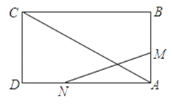
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】航模兴趣小组的老师想知道全组学生的年龄情况,于是让大家把自己的年龄写在纸上,下表是全组40名学生的年龄(单位:岁).
14 | 13 | 13 | 15 | 16 | 12 | 14 | 16 | 17 | 13 |
14 | 15 | 12 | 12 | 13 | 14 | 15 | 16 | 15 | 14 |
13 | 12 | 15 | 14 | 17 | 16 | 16 | 13 | 12 | 14 |
14 | 15 | 13 | 16 | 15 | 16 | 17 | 14 | 14 | 13 |
(1)在这个统计表中,13岁的频数是多少?频率是多少?
(2)多少岁的频率最大,这个最大频率是多少?
(3)假如老师随机地问一名学生的年龄,你认为老师最可能听到的回答是多少岁?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形OABC是矩形,点A的坐标为(3,0),点C的坐标为(0,6),点P从点O出发,沿OA以每秒1个单位长度的速度向点A出发,同时点Q从点A出发,沿AB以每秒2个单位长度的速度向点B运动,当点P与点A重合时运动停止.设运动时间为t秒.
(1)当t=2时,线段PQ的中点坐标为_____;
(2)当△CBQ与△PAQ相似时,求t的值;
(3)当t=1时,抛物线y=x2+bx+c经过P,Q两点,与y轴交于点M,抛物线的顶点为K,如图2所示,问该抛物线上是否存在点D,使∠MQD=![]() ∠MKQ?若存在,求出所有满足条件的D的坐标;若不存在,说明理由.
∠MKQ?若存在,求出所有满足条件的D的坐标;若不存在,说明理由.
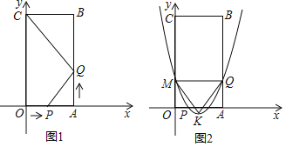
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究问题:一个不透明的盒中装有若干个白球,怎样估算白球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验.摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
统计结果如表:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到有记号球的次数m | 25 | 44 | 57 | 105 | 160 | 199 |
摸到有记号球的频率 | 0.25 | 0.22 | 0.19 | 0.21 | 0.20 | 0.20 |
(1)请你完成上表中数据,并估计摸到有记号球的概率是多少?
(2)估计盒中共有球多少个?没有记号球有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于点F,ME交BC于点G.写出图中的所有相似三角形,并选择一对加以证明.
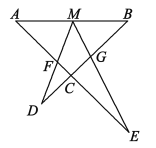
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年5月1日,目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,苏南A地到宁波港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.
(1)求跨海大桥到宁波港的路程.
(2)若货物运输费用=A地经杭州湾包括运输成本和时间成本,已知某车货物从A地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地.若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8320元,其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外其余均相同的红、蓝两种球,已知其中红球有3个,且从中任意摸出一个是红球的概率为0.75.
(1)根据题意,袋中有 个蓝球.
(2)若第一次随机摸出一球,不放回,再随机摸出第二个球.请用画树状图或列表法求“摸到两球中至少一个球为蓝球(记为事件A)”的概率P(A).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com