
【题目】2008年5月1日,目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,苏南A地到宁波港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.
(1)求跨海大桥到宁波港的路程.
(2)若货物运输费用=A地经杭州湾包括运输成本和时间成本,已知某车货物从A地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地.若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8320元,其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
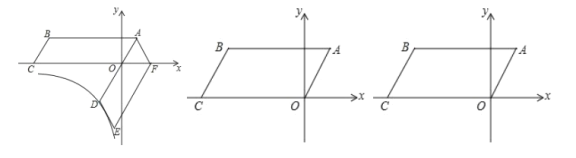
【题目】如图,在平面直角坐标系中,四边形![]() 为平行四边形,
为平行四边形,![]() 为坐标原点,
为坐标原点,![]() ,将平行四边形
,将平行四边形![]() 绕点
绕点![]() 逆时针旋转得到平行四边形
逆时针旋转得到平行四边形![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 落在
落在![]() 轴正半轴上.
轴正半轴上.
(1)证明:![]() 是等边三角形:
是等边三角形:
(2)平行四边形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 度
度![]() .
.![]() 的对应线段为
的对应线段为![]() ,点
,点![]() 的对应点为
的对应点为![]()
①直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标:
的坐标:
②对角线![]() 在旋转过程中设点
在旋转过程中设点![]() 坐标为
坐标为![]() ,当点
,当点![]() 到
到![]() 轴的距离大于或等于
轴的距离大于或等于![]() 时,求
时,求![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程![]() ,下列说法:①若a+c=0,方程
,下列说法:①若a+c=0,方程![]() 有两个不等的实数根;②若方程
有两个不等的实数根;②若方程![]() 有两个不等的实数根,则方程
有两个不等的实数根,则方程![]() 也一定有两个不等的实数根;③若c是方程
也一定有两个不等的实数根;③若c是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立;④若m是方程
成立;④若m是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立.其中正确地只有 ( )
成立.其中正确地只有 ( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,点
,点![]() .已知抛物线
.已知抛物线![]() (
(![]() 是常数),顶点为
是常数),顶点为![]() .
.
(Ⅰ)当抛物线经过点![]() 时,求顶点
时,求顶点![]() 的坐标;
的坐标;
(Ⅱ)若点![]() 在
在![]() 轴下方,当
轴下方,当![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(Ⅲ) 无论![]() 取何值,该抛物线都经过定点
取何值,该抛物线都经过定点![]() .当
.当![]() 时,求抛物线的解析式.
时,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
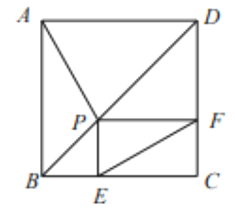
【题目】如图,己知正方形ABCD的边长为4, P是对角线BD上一点,PE⊥BC于点E, PF⊥CD于点F,连接AP, EF.给出下列结论:①PD=![]() EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF;⑤EF的最小值为
EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF;⑤EF的最小值为![]() ;⑥AP⊥EF.其中正确结论的序号为( )
;⑥AP⊥EF.其中正确结论的序号为( )
A. ①②④⑤⑥B. ①②④⑤
C. ②④⑤D. ②④⑤⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,连接AC、FC.
(1)求证:∠ACF=∠ADB;
(2)若点A到BD的距离为m,BF+CF=n,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
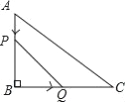
【题目】如图,在△ABC中,∠B=90°,BC=8 AB=6cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A. 18cm2 B. 12cm2 C. 9cm2 D. 3cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com