
【题目】如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,连接AC、FC.
(1)求证:∠ACF=∠ADB;
(2)若点A到BD的距离为m,BF+CF=n,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.

【答案】见解析
【解析】
(1)连接AB,根据线段垂直平分线性质求出AB=AC=AD,推出∠ADB=∠ABD,根据∠ABD=∠ACM求出即可;
(2)过点A作AH⊥BD于点H,求得∠FCD=∠FDC,根据勾股定理和等腰直角三角形的性质求出CD的平方,即可求出答案;
(3)过点D作DH⊥AO于N,过点D作DQ⊥BC于Q根据AAS证△DAM ≌△ACO和△DAF ≌△CAF,推出DH=AO,AH=OC,推出DQ=BQ,得出∠DBQ=45°,推出∠HDE=45°,得出等腰直角三角形DHE即可.
解:(1)证明:∵ PO⊥BC
∴ BO=CO
∴ AO垂直平分BC
∴ AB=AC
又∵ △ACD是以AC为直角边作等腰直角三角形
∴ AC= AD
∴ AB= AD
∴ ∠ABD=∠ADB
∵ ∠ABD=∠ACF
∴ ∠ACF =∠ADB
解:(2)过点A作AH⊥BD于点H
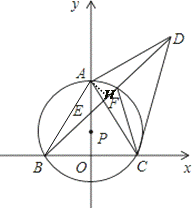
∴ AH=1
∵ △ACD是以AC为直角边作等腰直角三角形
∴ ∠ACD=∠ADC
∵ ∠ACF =∠ADB
∴∠ACD-∠ACF =∠ADC-∠ADB
即:∠FCD=∠FDC
∴ CF =DF
∵ BF+CF=14
∴ BD= BF+ DF = BF+CF =14
又∵ AB= AD
∴ BH= DH=![]() BD=7
BD=7
∴在Rt△ADH中:AD=![]()
∴ AC= AD![]()
∴ CD=![]()
解:(3)![]() 的值不发生变化,过点过点D作DM⊥y轴于点M
的值不发生变化,过点过点D作DM⊥y轴于点M
∴ ∠DMA=∠AOC=90°
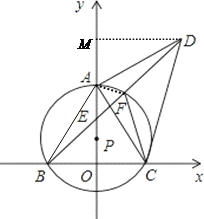
∴ ∠OAC+∠ACO=90°
∵ △ACD是以AC为直角边作等腰直角三角形
∴ ![]() ,∴ ∠DAC=90°,AC= AD
,∴ ∠DAC=90°,AC= AD
∴ ∠DAM +∠OAC = 90°
∴∠DAM=∠ACO
∴ △DAM ≌△ACO
∴ DM=AO
在△DAF与△CAF中,
AD=AC,AF=AF,DF=CF,
∴ △DAF ≌△CAF
∴ ∠DAF=∠CAF = 45°
∴ ∠CBF=∠CAF = 45°
∴ ∠BEO = 45°
∴ ∠DEM=∠BEO = 45°
∴ △DEM是等腰直角三角形
∴![]()
∴![]()
“点睛”本题考查了等腰直角三角形,全等三角形的性质和判,及勾股定理,线段垂直平分线性质,解(1)小题的关键是求出AB=AC=AD,解(2)小题的关键是求出BH的长,解(3)小题的关键是证出△DEM是等腰直角三角形.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】航模兴趣小组的老师想知道全组学生的年龄情况,于是让大家把自己的年龄写在纸上,下表是全组40名学生的年龄(单位:岁).
14 | 13 | 13 | 15 | 16 | 12 | 14 | 16 | 17 | 13 |
14 | 15 | 12 | 12 | 13 | 14 | 15 | 16 | 15 | 14 |
13 | 12 | 15 | 14 | 17 | 16 | 16 | 13 | 12 | 14 |
14 | 15 | 13 | 16 | 15 | 16 | 17 | 14 | 14 | 13 |
(1)在这个统计表中,13岁的频数是多少?频率是多少?
(2)多少岁的频率最大,这个最大频率是多少?
(3)假如老师随机地问一名学生的年龄,你认为老师最可能听到的回答是多少岁?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年5月1日,目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,苏南A地到宁波港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.
(1)求跨海大桥到宁波港的路程.
(2)若货物运输费用=A地经杭州湾包括运输成本和时间成本,已知某车货物从A地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地.若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8320元,其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
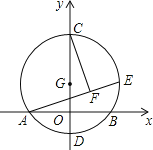
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E从B点出发顺时针运动到D点时,点F经过的路径长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)(x+8)2=36;
(2)x(5x+4)-(4+5x)=0;
(3)x2+3=3(x+1);
(4)2x2-x-1=0(用配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外其余均相同的红、蓝两种球,已知其中红球有3个,且从中任意摸出一个是红球的概率为0.75.
(1)根据题意,袋中有 个蓝球.
(2)若第一次随机摸出一球,不放回,再随机摸出第二个球.请用画树状图或列表法求“摸到两球中至少一个球为蓝球(记为事件A)”的概率P(A).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某政府在广场上树立了如图所示的宣传牌,数学兴趣小组的同学想利用所学的知识测量宣传牌的高度AB,在D处测得点A、B的仰角分别为38°、21°,已知CD=20m,点A、B、C在一条直线上,AC⊥DC,求宣传牌的高度AB(sin21°≈0.36,cos21°≈0.93,tan21°≈0.38,sin38°≈0.62,cos38°≈0.78,tan38°≈0.79,结果精确到1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了检验两枚六个面分别刻有点数1、 2、3、4、5、6的正六面体骰子的质量是否都合格,在相同的条件下,同时抛两枚骰子20 00 0次,结果发现两个朝上面的点数和是7的次数为20次.你认为这两枚骰子质量是否都合格(合格标准为:在相同条件下抛骰子时,骰子各个面朝上的机会相等)?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com