
【题目】在ABCD中,点E、F分别在AB、CD上,且AE=CF.
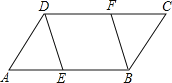
(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】给出下列说法:①三条线段组成的图形叫三角形;②三角形的角平分线是射线;③三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外;④任何一个三角形都有三条高、三条中线、三条角平分线;⑤三角形的三条角平分线交于一点,且这点在三角形内.正确的说法有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列多项式乘法,能用平方差公式进行计算的是( )
A. (x+y)(-x-y) B. (2x+3y)(2x-3z) C. (-a-b)(a-b) D. (m-n)(n-m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),B(0,4![]() ),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
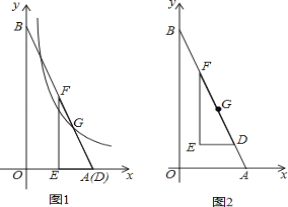
(1)求直线AB的解析式;
(2)如图1,当点D与点A重合时,求经过点G的反比例函数y=![]() (k≠0)的解析式;
(k≠0)的解析式;
(3)在三角尺滑动的过程中,经过点G的反比例函数的图象能否同时经过点F?如果能,求出此时反比例函数的解析式;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
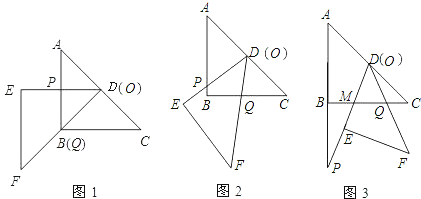
【题目】把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,APCQ= ;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问APCQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】命题“一个锐角的补角大于这个锐角的余角”的条件是_______________________,结论是____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com