分析:(1)先由二次函数的解析式求出点C的坐标,然后在Rt△BOC中,根据sin∠ABC的值得到点B的坐标,再将A、B两点的坐标代入抛物线的解析式,利用待定系数法求出解析式,通过对解析式进行配方即可得到顶点D的坐标;
(2)先利用待定系数法求出直线CD的解析式为y=x+8,那么可设Q点的坐标为(x,x+8).当以B,C,Q为顶点的三角形是等腰三角形时,分三种情况进行讨论:①BQ=BC;②CQ=BC;③QB=QC.然后针对每一种情况,根据两点间的距离公式列出方程,解方程即可;
(3)先求出直线CD:y=x+8与x轴的交点E的坐标,得到OC=OE=8,∠CEO=45°.设直线y=2x-4与直线CD交于点F,分两种情况进行讨论:①当点P在点F的下方时,过点P作PQ⊥x轴于点Q.根据四边形内角和定理求出∠MPQ=135°,根据三角形内角和定理求出∠POQ=30°,得到直线OP的解析式为y=
x,解方程组
即可求出点P的坐标;②当点P在点F的上方时,过点P作PQ⊥x轴于点Q,设直线CD与直线OP交于点G.根据三角形内角和定理及外角的性质得出∠GOQ=60°,得到直线OP的解析式为y=
x,解方程组
即可求出点P的坐标.
解答:解:(1)∵二次函数y=ax
2+bx+8(a≠0)的图象与y轴交与点C,
∴点C(0,8),即OC=8;
Rt△OBC中,BC=OC÷sin∠ABC=8÷
=4
,
OB=
=4,
则点B(4,0).
将A、B的坐标代入抛物线的解析式中,得:
.
解得
,
故抛物线的解析式:y=-x
2+2x+8=-(x-1)
2+9,顶点D(1,9);
(2)在直线CD上存在点Q,能够使以B,C,Q为顶点的三角形是等腰三角形.理由如下:
设直线CD的解析式为y=kx+m,
将C(0,8),D(1,9)代入,
得
,解得
,
则直线CD的解析式为y=x+8.
设Q点的坐标为(x,x+8).
以B,C,Q为顶点的三角形是等腰三角形时,分三种情况讨论:
①当BQ=BC=4
时,有(x-4)
2+(x+8)
2=80,
整理,得2x
2+8x=0,
解得x
1=-4,x
2=0(不合题意,舍去).
当x=-4时,x+8=4,即此时Q点的坐标为(-4,4);
②当CQ=BC=4
时,有x
2+(x+8-8)
2=80,
整理,得2x
2=80,
解得x
1=2
,x
2=-2
.
当x=2
时,x+8=2
+8,即此时Q点的坐标为(2
,2
+8);
当x=-2
时,x+8=-2
+8,即此时Q点的坐标为(-2
,-2
+8);
③当QB=QC时,有(x-4)
2+(x+8)
2=x
2+(x+8-8)
2,
整理,得8x+80=0,
解得x=-10.
当x=-10时,x+8=-2,即此时Q点的坐标为(-10,-2).
综上可知,在直线CD上存在点Q,能够使以B,C,Q为顶点的三角形是等腰三角形,此时点Q的坐标为(-4,4)或(2
,2
+8)或(-2
,-2
+8)或(-10,-2);
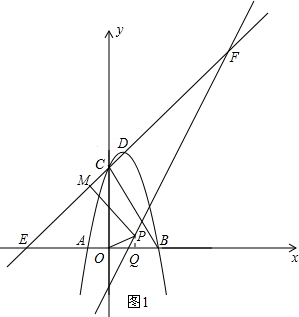
(3)设直线CD:y=x+8与x轴交于点E,则点E(-8,0),OC=OE=8,∠CEO=45°.
设直线y=2x-4与直线CD交于点F,分两种情况讨论:
①当点P在点F的下方时,如右图1,过点P作PQ⊥x轴于点Q.
在四边形EMPQ中,∠MPQ=360°-∠PME-∠PQE-∠MEQ=360°-90°-90°-45°=135°,
当∠MPO=75°时,∠OPQ=135°-75°=60°,∠POQ=30°,则直线OP的解析式为y=
x.
解方程组
,得
,
即此时P点的坐标为(
,
);
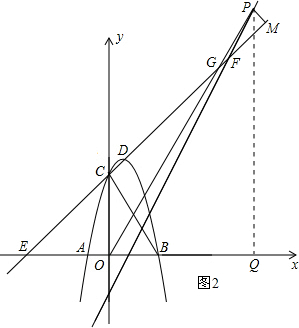
②当点P在点F的上方时,如右图2,过点P作PQ⊥x轴于点Q,设直线CD与直线OP交于点G.
在△MPG中,∠MGP=180°-∠PMG-∠GPM=180°-90°-75°=15°,
∴∠EGO=∠MGP=15°,
∴∠GOQ=∠GEO+∠EGO=45°+15°=60°,
∴直线OP的解析式为y=
x.
解方程组
,得
,
即此时P点的坐标为(8+4
,8
+12).
综上可知,点P的坐标为(
,
)或(8+4
,8
+12).

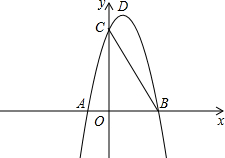 (2013•鞍山一模)如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交与A,B两点,与y轴交与点C,已知点A的坐标为(-2,0),sin∠ABC=
(2013•鞍山一模)如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交与A,B两点,与y轴交与点C,已知点A的坐标为(-2,0),sin∠ABC= 当x=-2
当x=-2 解方程组
解方程组

 导学全程练创优训练系列答案
导学全程练创优训练系列答案

 (2013•鞍山一模)在平行四边形ABCD中,∠DAB=60°,点E是AD的中点,点O是AB边上一点,且AO=AE,过点E作直线HF交DC于点H,交BA的延长线于F,以OE所在直线为对称轴,△FEO经轴对称变换后得到△F′EO,直线EF′交直线DC于点M.
(2013•鞍山一模)在平行四边形ABCD中,∠DAB=60°,点E是AD的中点,点O是AB边上一点,且AO=AE,过点E作直线HF交DC于点H,交BA的延长线于F,以OE所在直线为对称轴,△FEO经轴对称变换后得到△F′EO,直线EF′交直线DC于点M.
 (2013•鞍山一模)如图,在平面直角着坐标系中,一次函数y=
(2013•鞍山一模)如图,在平面直角着坐标系中,一次函数y=