
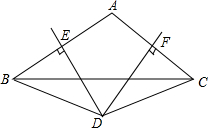
 如图,在△ABC中,DE垂直平分AB,DF垂直平分AC.
如图,在△ABC中,DE垂直平分AB,DF垂直平分AC.分析 (1)连接AD,利用垂直平分线的性质证明即可;
(2)利用三角形和四边形的内角和以及垂直平分线的性质解答即可.
解答 证明:(1)连接AD,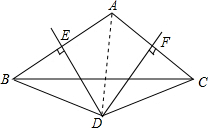
∵DE垂直平分AB,DF垂直平分AC,
∴BD=AD,AD=DC,
∴BD=DC,
∴△DBC是等腰三角形;
(2)∵DE垂直平分AB,DF垂直平分AC,
∴∠BDE=∠ADE,∠ADF=∠FDC,
∴∠EDF=$\frac{1}{2}$∠BDC,
∵∠ABC=30°,∠ACB=40°,
∴∠A=180°-30°-40°=110°,
∴∠EDF=180°-∠A=180°-110°=70°,
∴∠BDC=140°.
点评 此题考查等腰三角形的判定,关键是利用垂直平分线的性质解答.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 在一次高尔夫训练中,某球员从山坡下的点O打出一球,该球的飞行高度y(m)与飞行时间x(s)满足二次函数关系y=-$\frac{4}{27}$x2+bx,其函数图象如图所示,如果不考虑空气阻力,球的落点A距离点O的水平距离OB为12米时,垂直距离AB为$\frac{32}{3}$米.
在一次高尔夫训练中,某球员从山坡下的点O打出一球,该球的飞行高度y(m)与飞行时间x(s)满足二次函数关系y=-$\frac{4}{27}$x2+bx,其函数图象如图所示,如果不考虑空气阻力,球的落点A距离点O的水平距离OB为12米时,垂直距离AB为$\frac{32}{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,E为正方形ABCD外一点,连接BE
如图,E为正方形ABCD外一点,连接BE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时刻 | 8时 | 10时 | 12时 | 14时 | 16时 | 18时 |
| 体温 | 38.5 | 39.5 | 38 | |||
| 与正常人的正 常体温的差值 | +1.8 | +2.6 | +0.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com