
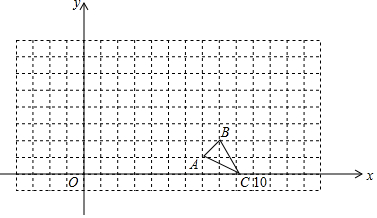
 在一次高尔夫训练中,某球员从山坡下的点O打出一球,该球的飞行高度y(m)与飞行时间x(s)满足二次函数关系y=-$\frac{4}{27}$x2+bx,其函数图象如图所示,如果不考虑空气阻力,球的落点A距离点O的水平距离OB为12米时,垂直距离AB为$\frac{32}{3}$米.
在一次高尔夫训练中,某球员从山坡下的点O打出一球,该球的飞行高度y(m)与飞行时间x(s)满足二次函数关系y=-$\frac{4}{27}$x2+bx,其函数图象如图所示,如果不考虑空气阻力,球的落点A距离点O的水平距离OB为12米时,垂直距离AB为$\frac{32}{3}$米.分析 (1)根据已知条件得到A(12,$\frac{32}{3}$),把A点代入y=-$\frac{4}{27}$x2+bx得到b=$\frac{8}{3}$,于是得到结论;
(2)把y=-$\frac{4}{27}$x2+$\frac{8}{3}$x配方得到y=-$\frac{4}{27}$(x-9)2+24,即可得到结论.
解答 解:(1)∵点A距离点O的水平距离OB为12米时,垂直距离AB为$\frac{32}{3}$米,
∴A(12,$\frac{32}{3}$),
把A点代入y=-$\frac{4}{27}$x2+bx得b=$\frac{8}{3}$,
∴y关于x的函数关系式为:y=-$\frac{4}{27}$x2+$\frac{8}{3}$x;
(2)∵y=-$\frac{4}{27}$x2+$\frac{8}{3}$x=-$\frac{4}{27}$(x-9)2+24,
∴该球飞行过程中的最大垂直高度是24米.
点评 本题考查了二次函数的应用及解直角三角形的知识,涉及了待定系数法求函数解析式的知识,注意建立数学模型,培养自己利用数学知识解决实际问题的能力,难度一般.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
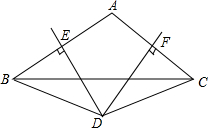 如图,在△ABC中,DE垂直平分AB,DF垂直平分AC.
如图,在△ABC中,DE垂直平分AB,DF垂直平分AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com