
【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.
【答案】(1)p=x+18;(2)第13天时当天的销售利润最大,最大销售利润是361元;(3)第7、8、9、10、11、12、13、14、15天共9天销售利润不低于325元
【解析】试题分析:(1)设p=kx+b(k≠0),然后根据第3天和第7天的成本利用待定系数法求一次函数解析式解答即可;
(2)根据销售利润=每盒的利润×盒数列出函数关系式,再根据一次函数的增减性和二次函数的最值问题求解;
(3)根据(2)的计算以及二次函数与一元二次方程的关系求解.
试题解析:(1)设p=kx+b(k≠0),∵第3天时,每盒成本为21元;第7天时,每盒成本为25元,∴![]() ,解得:
,解得: ![]() ,所以p=x+18;
,所以p=x+18;
(2)1≤x≤6时,w=10[50﹣(x+18)]=﹣10x+320,6<x≤15时,w=[50﹣(x+18)](x+6)=﹣x2+26x+192,所以,w与x的函数关系式为![]() ,
,
当1≤x≤6时,∵﹣10<0,∴w随x的增大而减小,∴当x=1时,w最大为﹣10+320=310,6<x≤15时,w=﹣x2+26x+192=﹣(x﹣13)2+361,∴当x=13时,w最大为361,
综上所述,第13天时当天的销售利润最大,最大销售利润是361元;
(3)w=325时,﹣x2+26x+192=325,x2﹣26x+133=0,解得x1=7,x2=19,所以,7≤x≤13时,即第7、8、9、10、11、12、13天共7天销售利润不低于325元.


科目:初中数学 来源: 题型:
【题目】某学校为了开展“阳光体育运动”,计划购买篮球与足球共![]() 个,已知每个篮球的价格为
个,已知每个篮球的价格为![]() 元,每个足球的价格为
元,每个足球的价格为![]() 元
元
(1)若购买这两类球的总金额为![]() 元,求篮球和足球各购买了多少个?
元,求篮球和足球各购买了多少个?
(2)元旦期间,商家给出蓝球打九折,足球打八五折的优惠价,若购买这种篮球与足球各![]() 个,那么购买这两类球一共需要多少钱?
个,那么购买这两类球一共需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点和它内部的点P1,把△ABC分成3个互不重叠的小三角形;△ABC的三个顶点和它内部的点P1、P2,把△ABC分成5个互不重叠的小三角形;△ABC的三个顶点和它内部的点 P1、P2、P3,把△ABC分成7个互不重叠的小三角形;…△ABC的三个顶点和它内部的点 P1、P2、P3、…、P2017,把△ABC分成_____个互不重叠的小三角形.
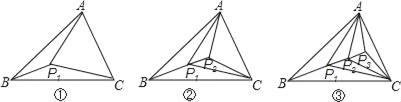
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2![]() .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE=![]() ,求图中阴影部分的面积;
,求图中阴影部分的面积;
(3)若![]() ,DF+BF=8,如图2,求BF的长.
,DF+BF=8,如图2,求BF的长.
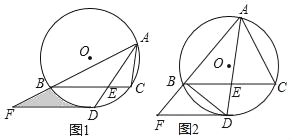
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
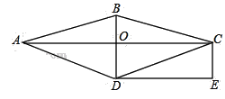
(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,求菱形ABCD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进甲、乙两种商品,已知甲的进价是乙的进价的一半,进3件甲商品和1件乙商品恰好用200元.甲、乙两种商品的售价每件分别为80元、130元,该商店决定用不少于6710元且不超过6810元购进这两种商品共100件.
(1)求这两种商品的进价.
(2)该商店有几种进货方案?哪种进货方案可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推动阳光体育活动的广泛开展,引导学生积极参加体育锻炼,学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据图中提供的信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 人,图①中的m的值为 ,图①中“38号”所在的扇形的圆心角度数为 ;
(2)本次调查获取的样本数据的众数是 ,中位数是 ;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买36号运动鞋多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区对即将参加中考的4 000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
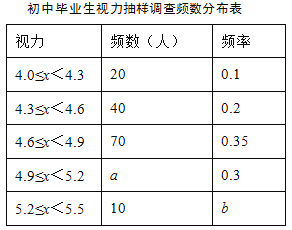
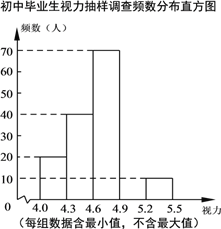
(1)本次调查样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )
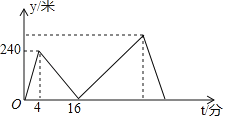
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com