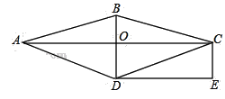
[题目]如图.在菱形ABCD中.对角线AC与BD交于点O．过点C作BD的平行线.过点D作AC的平行线.两直线相交于点E．(1)求证:四边形OCED是矩形,(2)若CE=1.DE=2.求菱形ABCD的面积. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在菱形ABCD中，对角线AC与BD交于点O．过点C作BD的平行线，过点D作AC的平行线，两直线相交于点E．

（1）求证：四边形OCED是矩形；（2）若CE=1，DE=2，求菱形ABCD的面积。

【答案】（1）见解析；（2）S菱形ABCD=4.

【解析】

（1）要证明四边形OCED是矩形，只需推知四边形OCED是平行四边形，且有一内角为90度即可；

（2）由菱形的对角线互相垂直平分和菱形的面积公式解答．

解：（1）证明：∵CE//BD,DE//AC

∴四边形ODEC为平行四边形

∵四边形ABCD是菱形

∴AC⊥BD

∴∠COD=90°

∴四边形ODEC为矩形.

（2）由（1）知，平行四边形OCED是矩形，则CE=OD=1，DE=OC=2．

∵四边形ABCD是菱形，

∴AC=2OC=4，BD=2OD=2，

∴菱形ABCD的面积为：ACBD=×4×2=4．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】阅读下面材料：

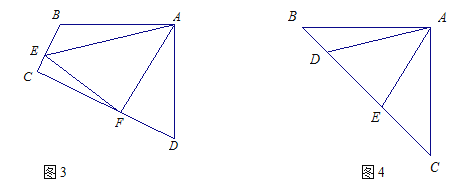
小炎遇到这样一个问题：如图1，点E、F分别在正方形ABCD的边BC，CD上，∠EAF=45°，连结EF，则EF=BE+DF，试说明理由．

小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中．她先后尝试了翻折、旋转、平移的方法，最后发现线段AB，AD是共点并且相等的，于是找到解决问题的方法．她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG，再利用全等的知识解决了这个问题（如图2）．

参考小炎同学思考问题的方法，解决下列问题：

（1）如图3，四边形ABCD中，AB=AD，∠BAD=90°点E，F分别在边BC，CD上，∠EAF=45°．若∠B，∠D都不是直角，则当∠B与∠D满足_ 关系时，仍有EF=BE+DF；

（2）如图4，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°，若BD=1， EC=2，求DE的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某校将举行“亲近大自然”户外活动．现随机抽取了部分学生进行了“你最想去的景点”的问卷调查，要求学生只能从A，B，C，D四个景点中选择一个．根据调查结果，绘制了如下两幅不完整的统计图．

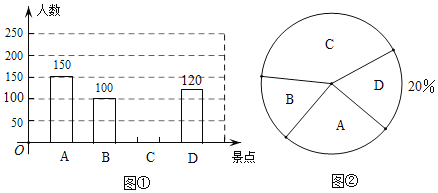
（1）本次调查共调查了______名学生；

（2）补全图①中的条形统计图，图②中最想去景点C的圆心角的度数为______°．

（3）已知该校共有2400名学生，估计最想去景点C的学生人数．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】A，B两地间仅有一长为180千米的平直公路，若甲，乙两车分别从A，B两地同时出发匀速前往B，A两地，乙车速度是甲车速度的倍，乙车比甲车早到45分钟．

（1）求甲车速度；

（2）乙车到达A地停留半小时后以来A地时的速度匀速返回B地，甲车到达B地后立即提速匀速返回A地，若乙车返回到B地时甲车距A地不多于30千米，求甲车至少提速多少千米/时？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知直线y=kx+b经过点A（3，7）和B（﹣8，-4）．

（1）求直线的解析式；

（2）求出该直线与x轴、y轴的交点坐标。并求出直线与两坐标轴围成三角形的面积。

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀．小张购进一批食材制作特色美食，每盒售价为50元，由于食材需要冷藏保存，导致成本逐日增加，第x天（1≤x≤15且x为整数）时每盒成本为p元，已知p与x之间满足一次函数关系；第3天时，每盒成本为21元；第7天时，每盒成本为25元，每天的销售量为y盒，y与x之间的关系如下表所示：