
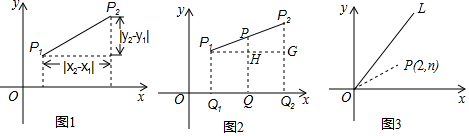
分析 (1)用P1、P2的坐标分别表示出OQ和PQ的长即可证得结论;
(2)①直接利用两点间距离公式可求得MN的长;②分AB、AC、BC为对角线,可求得其中心的坐标,再利用中点坐标公式可求得D点坐标;
(3)设P关于直线OL的对称点为M,关于x轴的对称点为N,连接PM交直线OL于点R,连接PN交x轴于点S,则可知OR=OS=2,利用两点间距离公式可求得R的坐标,再由PR=PS=n,可求得n的值,可求得P点坐标,利用中点坐标公式可求得M点坐标,由对称性可求得N点坐标,连接MN交直线OL于点E,交x轴于点S,此时EP=EM,FP=FN,此时满足△PEF的周长最小,利用两点间距离公式可求得其周长的最小值.
解答 解:
(1)∵P1(x1,y1),P2(x2,y2),
∴Q1Q2=OQ2-OQ1=x2-x1,
∴Q1Q=$\frac{{x}_{2}-{x}_{1}}{2}$,
∴OQ=OQ1+Q1Q=x1+$\frac{{x}_{2}-{x}_{1}}{2}$=$\frac{{{x_1}+{x_2}}}{2}$,
∵PQ为梯形P1Q1Q2P2的中位线,
∴PQ=$\frac{{P}_{1}{Q}_{1}+{P}_{2}{Q}_{2}}{2}$=$\frac{{{y_1}+{y_2}}}{2}$,
即线段P1P2的中点P(x,y)P的坐标公式为x=$\frac{{{x_1}+{x_2}}}{2}$,y=$\frac{{{y_1}+{y_2}}}{2}$;
(2)①∵M(2,-1),N(-3,5),
∴MN=$\sqrt{(2+3)^{2}+(-1-5)^{2}}$=$\sqrt{61}$,
故答案为:$\sqrt{61}$;
②∵A(2,2),B(-2,0),C(3,-1),
∴当AB为平行四边形的对角线时,其对称中心坐标为(0,1),
设D(x,y),则x+3=0,y+(-1)=2,解得x=-3,y=3,
∴此时D点坐标为(-3,3),
当AC为对角线时,同理可求得D点坐标为(7,1),
当BC为对角线时,同理可求得D点坐标为(-1,-3),
综上可知D点坐标为(-3,3)或(7,1)或(-1,-3),
故答案为:(-3,3)或(7,1)或(-1,-3);
(3)如图,设P关于直线OL的对称点为M,关于x轴的对称点为N,连接PM交直线OL于点R,连接PN交x轴于点S,连接MN交直线OL于点E,交x轴于点F,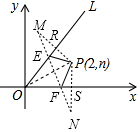
又对称性可知EP=EM,FP=FN,
∴PE+PF+EF=ME+EF+NF=MN,
∴此时△PEF的周长即为MN的长,为最小,
设R(x,$\frac{4}{3}$x),由题意可知OR=OS=2,PR=PS=n,
∴$\sqrt{{x}^{2}+(\frac{4}{3}x)^{2}}$=2,解得x=-$\frac{6}{5}$(舍去)或x=$\frac{6}{5}$,
∴R($\frac{6}{5}$,$\frac{8}{5}$),
∴$\sqrt{(2-\frac{6}{5})^{2}+(n-\frac{8}{5})^{2}}$=n,解得n=1,
∴P(2,1),
∴N(2,-1),
设M(x,y),则$\frac{x+2}{2}$=$\frac{6}{5}$,$\frac{y+1}{2}$=$\frac{8}{5}$,解得x=$\frac{2}{5}$,y=$\frac{11}{5}$,
∴M($\frac{2}{5}$,$\frac{11}{5}$),
∴MN=$\sqrt{(2-\frac{2}{5})^{2}+(-1-\frac{11}{5})^{2}}$=$\frac{8\sqrt{5}}{5}$,
即△PEF的周长的最小值为$\frac{8\sqrt{5}}{5}$.
点评 本题为一次函数的综合应用,涉及中位线定理、中点坐标公式、两点间距离公式、轴对称的性质、角平分线的性质、平行四边形的性质等知识.在(1)中求得OQ和PQ的长是解题的关键,在(2)中注意中点坐标公式的应用,在(3)中确定出E、F的位置,求得P点的坐标是解题的关键.本题考查知识点较多,综合性较强,计算量较大,难度较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.767×105 | B. | 6.767×1012 | C. | 6.767×1013 | D. | 6.767×1014 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
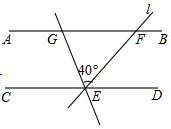 如图,已知直线AB∥CD,直线l与直线AB、CD相交于点,E、F,将l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=70°,那么∠GFE=70度.
如图,已知直线AB∥CD,直线l与直线AB、CD相交于点,E、F,将l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=70°,那么∠GFE=70度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com