
【题目】如图,在矩形ABCD中,AB=10cm,BC=4cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D停止,当运动时间为秒时,△MBN为等腰三角形. 
【答案】![]() 或(12﹣4
或(12﹣4 ![]() )或
)或 ![]()
【解析】解:①如图1, 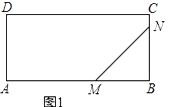
点M在AB上,点N在BC上时,t<4,BM=10﹣2t,BN=t,
∵BM=BN,
∴10﹣2t=t,
解得t= ![]() ,
,
②如图2,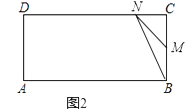
点M在BC上,点N在CD上时,5<t<7,BM=2t﹣10,CM=4﹣(2t﹣10)=14﹣2t,
CN=t﹣4,
在Rt△MCN中,MN2=(14﹣2t)2+(t﹣4)2 ,
∵BM=MN,
∴(2t﹣10)2=(14﹣2t)2+(t﹣4)2 ,
整理得,t2﹣24t+112=0,
解得t1=12﹣4 ![]() ,t2=12+4
,t2=12+4 ![]() (舍去),
(舍去),
③如图3,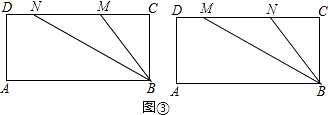
点M、N都在C、D上时,t>7,若点M在点N的右边,则CM=2t﹣14,MN=t﹣(2t﹣14)=14﹣2t,
此时BM2=(2t﹣14)2+42 ,
∵BM=MN,
∴(2t﹣14)2+42=(14﹣2t)2 , 无解,
若点M在点N的左边,则CN=t﹣4,
MN=(2t﹣14)﹣(t﹣4)=t﹣10,
此时BN2=(t﹣4)2+42 ,
∵BN=MN,
∴(t﹣4)2+42=(t﹣10)2 ,
整理得,t= ![]() (不符合题意,舍去),
(不符合题意,舍去),
④如图④,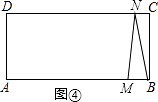
点M在AB上,点N在CD上时,BM=10﹣2t,CN=t﹣4,
由等腰三角形三线合一的性质,CN= ![]() BM,
BM,
所以,t﹣4= ![]() (10﹣2t),
(10﹣2t),
解得t= ![]() ,
,
综上所述,当运动时间为 ![]() 或(12﹣4
或(12﹣4 ![]() )或
)或 ![]() 秒时,△MBN为等腰三角形.
秒时,△MBN为等腰三角形.
故答案为: ![]() 或(12﹣4
或(12﹣4 ![]() )或
)或 ![]() .
.
分①点M在AB上,点N在BC上时,BM=BN,列出方程其解即可,②点M在BC上,点N在CD上时,表示出BM、CM、CN,再根据勾股定理列式表示出MN2 , 然后根据BM=MN列出方程其解即可;③点M、N都在C、D上时,表示出MN、CM,再根据勾股定理分两种情况列式表示出BM(或BN),然后根据BM=MN(或BN=MN)列出方程求解即可,④点M在AB上,点N在CD上时,根据等腰三角形的性质,CN= ![]() BM,然后列式求解即可.
BM,然后列式求解即可.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动.已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s). 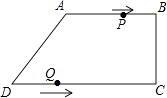
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某铁路桥长500m,现在一列火车匀速通过该桥,火车从开始上桥到过完桥共用了30s,整列火车完全在桥上的时间为20s,则火车的长度为多少m?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,桌面内,直线l上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为60°.将△ECD沿直线l向左平移到图的位置,使E点落在AB上,即点E′,点P为AC与E′D′的交点.
(1)求∠CPD′的度数;
(2)求证:AB⊥E′D′.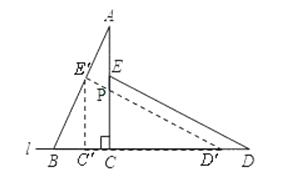
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com