
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]()
B.![]()
C.![]()
D.![]()
科目:初中数学 来源: 题型:
【题目】学校开展捐书活动,以下是5名同学捐书的册数:4,9,5,x,3,已知这组数据的平均数是5,则这组数据的中位数和众数分别是( )
A. 3和3 B. 4和4 C. 3和4 D. 5和5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论: ①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE ,
其中正确结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现: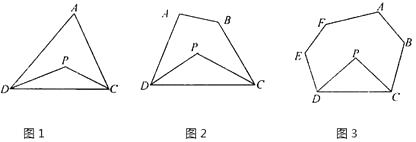
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,
试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=10cm,BC=4cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D停止,当运动时间为秒时,△MBN为等腰三角形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区2016年屋顶绿化面积为2000平方米,计划2018年屋顶绿化面积要达到2880平方米,如果每年屋顶绿化面积的增长率相同,那么这个增长率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如果把图中任一条线段沿方格线平移1格称为“1步”,那么要通过平移使图中的3条线段首尾相接组成一个三角形,最少需要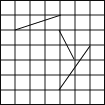
A.4步
B.5步
C.6步
D.7步
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com