
����Ŀ�����ı���ABCD�У�AB��CD����BCD=90�㣬AB=AD=10cm��BC=8cm����P�ӵ�A������������ABCD������3cm/s���ٶ������˶�����Q�ӵ�D���������߶�DC������2cm/s���ٶ������˶�����֪����ͬʱ��������һ���㵽���յ�ʱ����һ��Ҳֹͣ�˶������˶�ʱ��Ϊt��s���� 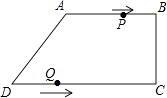
��1����CD�ij���
��2�����ı���PBQDΪƽ���ı���ʱ�����ı���PBQD���ܳ���
��3���ڵ�P��Q���˶������У��Ƿ����ijһʱ�̣�ʹ�á�BPQ�����Ϊ20cm2�������ڣ��������������������t��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��ͼ1��
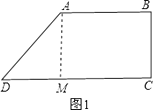
��A��AM��DC��M��
�����ı���ABCD�У�AB��CD����BCD=90�㣬
��AM��BC��
���ı���AMCB�Ǿ��Σ�
��AB=AD=10cm��BC=8cm��
��AM=BC=8cm��CM=AB=10cm��
��Rt��AMD�У��ɹ��ɶ����ã�DM=6cm��
CD=DM+CM=10cm+6cm=16cm
��2���⣺��ͼ2��
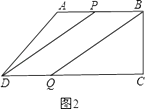
���ı���PBQD��ƽ���ı���ʱ��PB=DQ��
��10��3t=2t��
���t=2��
��ʱDQ=4��CQ=12��BQ= ![]() =
= ![]() ��
��
����C��PBQD=2��BQ+DQ��= ![]() ��
��
���ı���PBQD���ܳ��ǣ�8+8 ![]() ��cm
��cm
��3���⣺��P��AB��ʱ����ͼ3��
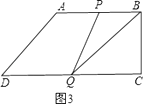
�� ![]() ��
��
S��BPQ= ![]() BPBC=4��10��3t��=20��
BPBC=4��10��3t��=20��
��� ![]() ��
��
��P��BC��ʱ����ͼ4���� ![]() ��
��
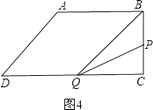
S��BPQ= ![]() BPCQ=
BPCQ= ![]() ��3t��10����16��2t��=20����
��3t��10����16��2t��=20����
�˷���û��ʵ���⣻
��P��CD��ʱ��
����P�ڵ�Q���Ҳ࣬��ͼ5���� ![]() ��
��
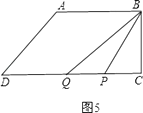
S��BPQ= ![]() PQBC=4��34��5t��=20��
PQBC=4��34��5t��=20��
��� ![]() ���������⣬Ӧ��ȥ��
���������⣬Ӧ��ȥ��
��P��Q����࣬��ͼ6���� ![]() ��
��
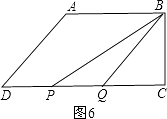
S��BPQ= ![]() PQBC=4��5t��34��=20��
PQBC=4��5t��34��=20��
��� ![]() ��
��
������������ ![]() ���
��� ![]() ��ʱ����BPQ�����Ϊ20cm2
��ʱ����BPQ�����Ϊ20cm2
����������1����A��AM��DC��M���ó�ƽ���ı���AMCB�����AM�����ݹ��ɶ������DM���ɣ���2������ƽ���ı��εĶԱ���ȵó����̣�������ɣ���3����Ϊ����������������⻭����������������ͼ�Σ����������ε�����ó����̣�������Ϸ�Χ�������ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������һ�Ρ����˻ᡱ֪ʶ�����������ȡ���ֲ���ͬѧ�ijɼ�������������������ͼ�����£�
������ | Ƶ�� | Ƶ�� |
��һ�飺60��x��70 | 30 | 0.15 |
�ڶ��飺70��x��80 | m | 0.45 |
�����飺80��x��90 | 60 | n |
�����飺90��x��100 | 20 | 0.1 |
�������ͼ���ṩ����Ϣ������������⣺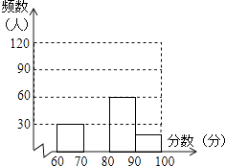
��1��д��������m��n����ʾ������m= �� n=��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����ȡ���ֲ���ͬѧ�ijɼ�����λ�����ڵ��飻
��4����������ɼ�80�����ϣ���80�֣����Ի�ý�������ô�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2012�Ĵ��Ű�)��ƽ��ֱ������ϵ�У�������ABC��������������ֱ���A(4��5)��B(1��2)��C(4��2)����������ABC����ƽ��5����λ��A��Ķ�Ӧ��A���������( )
A��(0��5)
B��(��1��5)
C��(9��5)
D��(��1��0)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ��չ������������5��ͬѧ����IJ�����4��9��5��x��3����֪�������ݵ�ƽ������5�����������ݵ���λ���������ֱ��ǣ� ��
A. 3��3 B. 4��4 C. 3��4 D. 5��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��x����5�������ĸ����̵Ľ⣨������
A. x��1��6B. 2x��5��2C. 2��3x��17D. x2��1��26
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����д���н�������е��������ݣ�
��֪����ͼ����F��E�ֱ���AB��CD�ϣ�AE��DF�ֱ���BC�ཻ��H��G����A����D����1����2��180��.˵����AB��CD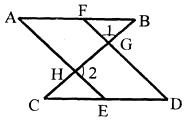
�⣺�ߡ�1����CGD����
��1����2��180��
��.
��AE//FD ����
������ֱ��ƽ�У�ͬλ����ȣ�
�֡�A����D
���D����BFD
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���2x2��5x��4��0��������ǣ�������
A. ����������ȵ�ʵ����
B. ��������ȵ�ʵ����
C. û��ʵ����
D. ���ж��÷��̸������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABCD�У�AEƽ�֡�BAD��BC��E����CAE=15�㣬������Ľ��ۣ� �١�ODC�ǵȱ������Σ���BC=2AB���ۡ�AOE=135�㣻��S��AOE=S��COE ��
������ȷ�����У� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=10cm��BC=4cm��M��N����ֱ��A��B������2cm/s��1cm/s���ٶ��ھ���ABCD��������ʱ�뷽���˶���������һ���˶�����Dֹͣ�����˶�ʱ��Ϊ��ʱ����MBNΪ���������Σ� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com