
【题目】(10)已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O 相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线l与⊙O 相交于点E、F时,若∠DAE=18°,求∠BAF的大小.

【答案】(1)30°;(2)18°.
【解析】试题分析:(1)如图①,首先连接OC,由当直线l与⊙O相切于点C,AD⊥l于点D.易证得OC∥AD,继而可求得∠BAC=∠DAC=30°;
(2)如图②,连接BF,由AB是⊙O的直径,由直径所对的圆周角是直角,可得∠AFB=90°,由三角形外角的性质,可求得∠AEF的度数,又由圆的内接四边形的性质,求得∠B的度数,继而求得答案.
试题解析:解:(1)如图①,连接OC,∵直线l与⊙O相切于点C,∴OC⊥l,∵AD⊥l,∴OC∥AD,∴∠OCA=∠DAC,∵OA=OC,∴∠BAC=∠OCA,∴∠BAC=∠DAC=30°;
(2)如图②,连接BF,∵AB是⊙O的直径,∴∠AFB=90°,∴∠BAF=90°﹣∠B,∴∠AEF=∠ADE+∠DAE=90°+18°=108°,在⊙O中,四边形ABFE是圆的内接四边形,∴∠AEF+∠B=180°,∴∠B=180°﹣108°=72°,∴∠BAF=90°﹣∠B=90°﹣72°=18°.
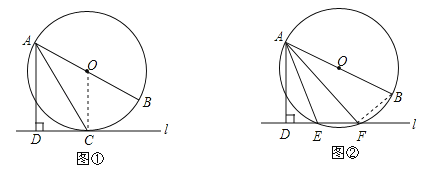


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,点C是![]() 中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E
中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E

(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-![]() x2+x+4.
x2+x+4.
(1)确定抛物线的开口方向、顶点坐标和对称轴;
(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
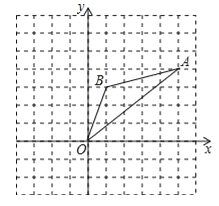
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1.
(1)画出△A1OB1;
(2)在旋转过程中点B所经过的路径长为 ;
(3)求在旋转过程中线段AB、BO扫过的图形的面积之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com